При вычислении значений многочленов вида на ЭВМ
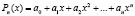
приходится проводить расчёты «в лоб», но при больших значениях п число вычислительных операций равно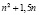 
. Кроме того, при реализации вычислительного процесса могут возникнуть неточности за счёт погрешностей округления. Для исключения этих недостатков применяется схема Горнера – алгоритм вычисления значения многочлена, записанного в виде суммы одночленов
.
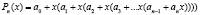Метод Горнера позволяет отыскать корни многочлена и вычислить производные полинома в заданной точке. Схема Горнера является простым алгоритмом для деления многочлена на бином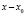 
. Использование этого метода не только экономит машинное время (требуется 2n вычислительных операций), но и увеличивает точность вычислительного процесса за счёт уменьшения машинных (компьютерных) погрешностей.
Алгоритм вычислительного процесса можно представить в виде блок-схемы.
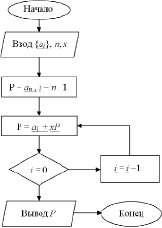
Приведём основную часть практической реализации вычисления значения полинома с помощью схемы Горнера
do
{ k = 5;
cout << endl;
if (k / size == 0)
d = k %size;
for (int i = count; i<d + count; i++)
cout << setw(8) << a[i];
cout << endl;
for (int s = 0; s<60; s++)
cout << «_»;
cout << endl;
for (int i = count; i < d + count; i++)
P += a[i];
for (int i = count; i < d + count; i++)
cout << setw(8) << a_sum[i];
cout << endl;
k -= d;
count += size;
} while (k != 0);
cout << endl;
delete[]a;
delete[]a_mul;
delete[]a_sum;
for (int s = 0; s < 80; s++) {cout << «=»;}
cout << endl<<»P(«<<x<<»)=»<<P<<endl;
cout << endl<< endl;
_getch();
return 0;
}