Многочлены Чебышёва первого рода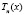 
могут быть определены с помощью рекуррентных соотношений:
, 
, …,
.
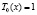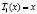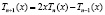Первые многочлены Чебышёва имеют вид:
, 
,
, 
,
,
,
,
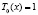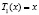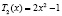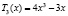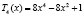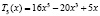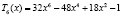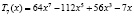, и т.д.
В работе рассматривается аппроксимация экспериментальных зависимостей с помощью ортогональных полиномов Чебышёва, которые преобразованы в алгебраические многочлены. Такие многочлены легко вычислять, дифференцировать и интегрировать.
Пусть необходимо аппроксимировать экспериментальную зависимость вида:
|
xi |
x1 |
x2 |
… |
xi |
… |
xn |
|
yi |
y1 |
y2 |
… |
yi |
… |
yn |
xi – значения входных параметров исследуемого процесса, xi – значения выходных параметров исследуемого процесса. Аппроксимирующую функцию будем искать в виде суммы многочленов Чебышёва, т.е.
.
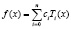Используя узловые точки, запишем формулу для вычисления коэффициентов
.
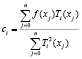Процедуры, написанные средствами системы Mathcad 15, позволяют рассчитывать их коэффициенты.
Для исходных данных
|
xi |
5 |
10 |
20 |
30 |
40 |
50 |
|
yi |
45 |
30 |
35 |
30 |
25 |
20 |
была получена приближающая функция. На графике (рис. 1) изображены экспериментальные данные в виде точек и аппроксимирующий многочлен.
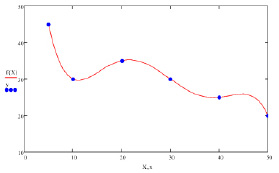
Графики экспериментальных и теоретических зависимостей наглядно доказывают хорошее качество аппроксимации.