Изучая какое-либо явление, мы должны, прежде всего, создать его математическую модель. Зачастую это можно сделать с помощью дифференциальных уравнений. Математическая модель даёт возможность изучать явление в целом, а также спрогнозировать его развитие с течением времени. Теория дифференциальных уравнений представляет собой раздел математики, тесно связанный с другими областями математики и с её приложениями.
Как известно, многие экономические процессы взаимосвязаны. Любому из них свойственен циклический характер. Часто для исследования таких экономических систем, где независимой переменной является время Т, применяются дифференциальные уравнения.
Рассматрим применение дифференциальных уравнений 1-го порядка в моделях экономики на примере неоклассической модели роста. Пусть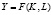 
– национальный доход, где F – однородная производственная функция первого порядка 
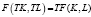, K – объём капиталовложений (производственных фондов), L – объём затрат труда.
Величина фондовооружённости выражается формулой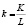 
.
Производительность труда выражается формулой
. (1)
Динамика фондовооружённости есть функция от времени Т. Для описания модели необходимо ввести параметры.
Естественный прирост во времени трудовых ресурсов
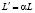. (2)
Инвестиции, расходуемые на увеличение производственных фондов и на амортизацию
,
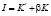где b – норма амортизации. Причём, если l – норма инвестиций, то
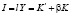или 
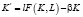. (3)
Из определения фондовооружённости К вытекает, что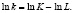 
Продифференцируем это равенство по переменной Т
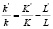. (4)
Подставляя выражения (2) и (3) в равенство (4), получаем уравнение относительно неизвестной функции k:
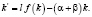(5)
Равенство (5) представляет собой нелинейное дифференциальное уравнение 1-го порядка с разделяющимися переменными. Т.к. по условию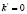 
, то
.
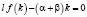Таким образом,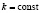 
– постоянная величина, являющаяся корнем этого нелинейного алгебраического уравнения.
Применение данного метода можно рассмотреть на примере конкретной задачи. Для уравнения (5) найдём интегральные кривые. Исходя из уравнения (1), получаем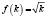 
. При этом уравнение (5) принимает вид:
.
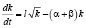Для найденного уравнения определим стационарное решение
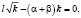
Отсюда получим частное решение уравнения (5)
.
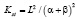Разделим переменные в (5) и решим полученное дифференциальное уравнение:
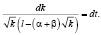
Проинтегрируем обе части, получим общее решение в виде:
.
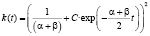Заметим, что интегральные кривые сходятся к стационарному решению (рисунок), то есть
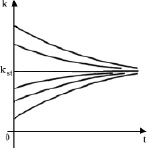
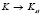при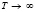 
.
Таким образом, если параметры задачи L, a и b фиксированны, то независимо от начальных условий функция фондовооружённости стремится к стационарному положению. Стационарная точка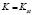 
– есть точка устойчивого равновесия.