В школьной математике есть базовая тема – решение квадратных уравнений во множестве действительных чисел.
В классах с углубленным изучением математики и институтах вводится понятие множества комплексных чисел и тогда справедливо утверждение, что всякий многочлен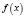 
степени n, 
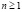с действительными коэффициентами имеет n корней, если каждый из корней считать столько раз, какова его кратность.
Тогда квадратное уравнение будет иметь ровно два корня, независимо от знака дискриминанта.
Задача 1. В классе может найтись ученик, который скажет: «Докажите, что нет ни одного квадратного уравнения с тремя различными корнями?»
Решение. Предположим, что мы всерьез ищем такое квадратное уравнение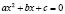 
, которому удовлетворяли бы три числа m, n, p. Подставляя числа m, n, p последовательно в уравнение, мы находим, что они будут удовлетворять этому уравнению, если
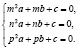
Для того чтобы числа (m, n, p) были корнями настоящего квадратного уравнения (уравнения отличного от тривиального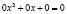 
), система полученных трех однородных уравнений относительно трех неизвестных (a, b, c) должна иметь ненулевое решение, а для этого ее определитель должен равняться нулю, то есть должно выполняться следующее условие
.
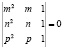Чтобы вычислить определитель, проведем его элементарные преобразования: вычтем из первой и второй строчек третью строку. Элементарные преобразования не изменяют значения определителя, но теперь его легко свести к определителю второго порядка, разложив по третьему столбцу, в котором после преобразования получилось два нуля.
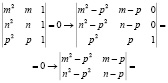
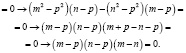
Итак, определитель равен
,
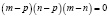откуда следует, что и требовалось доказать m=n или m=p или n=p. Сенсации не состоялось, квадратное уравнение не может иметь трех различных корней.
Но так ли уж все безнадежно с количеством корней?
Задача 2. Составьте хотя бы одно уравнение второй степени, которое имеет четыре различных корня.
Решение. Рассмотрим квадратное уравнение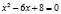 
. Его корни легко найти, решая уравнение через дискриминант или же по теореме Виета: 
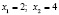. То есть, это уравнение имеет только два корня.
А теперь проделаем с этим уравнением «фокус» – поставим вокруг х две небольшие палочки, которые в математике означают модуль числа
.
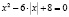По определению модуля
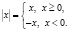
Поэтому характеристической точкой разбивающей область допустимых значений будет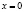 
, получается два интервала:
а) Пусть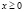 
, тогда уравнение, освобождаясь от модуля, принимает вид 
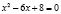, решая его обычным образом, находим корни 
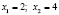. Оба корня попадают в рассматриваемый интервал.
б) Пусть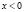 
, тогда, раскрывая модуль по определению, получаем иное квадратное уравнение 
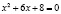, корнями которого будут числа 
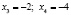, которые тоже попадают во второй интервал.
Таким образом, окончательное решение уравнения состоит из четырех корней:
, 
.
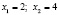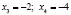Ответ: уравнение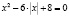 
имеет 4 различных корня 
, 
.
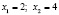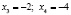Этого кстати можно было ожидать еще до решения, так как трехчлен, стоящий в левой части уравнения представляет собой четную функцию, следовательно, его корни должны быть симметричны относительно начала координат.
Все наши предыдущие рассуждения сводились к тому, что квадратное уравнение имеет два и только два корня, а вот вам уравнение с четырьмя корнями. Никто ведь отдельно не подчеркивает, есть ли в уравнении знак модуля. Но не зря в условии задачи написано не квадратное уравнение, а уравнение второй степени. В этом вся тонкость. По определению квадратное уравнение имеет вид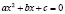 
, то есть, в нем модуля нет, а полученное нами уравнение – это уравнение второй степени, но не квадратное.