В учебные дни столовую посещают 100 студентов, которые идут обедать на большой перемене. Имеется две столовые: одна в институте, другая – недалеко от него. Каждый студент с равными вероятностями независимо от выбора других решает, в какую столовую пойти. Директор института желает, чтобы с вероятностью 0,99 все пришедшие студенты могли там одновременно пообедать. Поэтому возникает вопрос, какое количество мест для этого необходимо?
Будем считать, что событие А произошло, если студент пообедал в столовой при институте. По условию задачи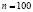 
, 
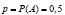. Нас интересует такое наименьшее число посетителей m, что вероятность одновременного прихода не менее чем m студентов из числа 
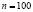с вероятностью успеха 
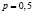приблизительно равна вероятности переполнения столовой, то есть 
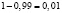. Таким образом, нас интересует такое наименьшее число m, что.
Подобные задачи решаются с применением интегральной теоремы Муавра-Лапласа для интервала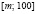 
. Т.к. 
, 
, 
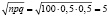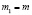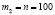, то
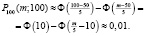
Отсюда получаем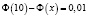 
или
.
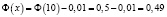Используя таблицу значений функции Лапласа Ф(x), находим,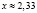 
, значит, 
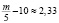. Из этого следует, что 
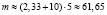. Следовательно, в столовой при институте должно быть как минимум 62 места.