Жители мегаполисов всё более часто производят покупки в интернет-магазинах. Для интернет-магазинов можно выделить характеристики, важные потенциальному покупателю: цена, качество товара, скорость доставки, ответственность выполнения обязательств. Последние можно обобщить и назвать надёжностью данного интернет-магазина.
Мы исследуем надёжность интернет-магазинов, которую будем определять по десятибалльной шкале. Шкалу надёжности магазинов определим по следующим образом: 1–2 – ненадёжный интернет-магазин; 3–4 – слабо надёжный; 5–6 – средне надёжный; 7-8 – надёжный, 9–10 – полностью надёжный. Для нахождения средней надёжности интернет-магазинов было выбрано на сайте Яндекс.Маркете 50 популярных интернет-магазинов и отзывы о них. Распределение числа интернет магазинов и степень их надёжности представлено в табл. 1.
Таблица 1
|
Шкала надёжности (балл) |
(0;2] |
(2;4] |
(4;6] |
(6;8] |
(8;10] |
|
|
Число магазинов, (частота ni) |
2 |
9 |
17 |
19 |
3 |
n=50 |
Предполагая, что Х – стоимость компьютера, является непрерывной случайной величиной, вычислим среднее значение надёжности выбранных интернет-магазинов (выборочное среднее), какой разброс составляют значения относительно среднего значения (исправленное выборочное среднеквадратичное отклонение), построим полигон для наглядности распределения, найдём диапазон значений надёжности относительно средней оценки (доверительный интервал для генеральной средней) с вероятностью 0,95.
Выборочное среднее:
,
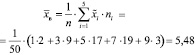где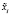 
– середины частичных интервалов. Таким образом, средняя оценка надёжности выбранных интернет-магазинов равна 5,48.
Найдём выборочную дисперсию:
.
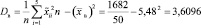Выборочное среднеквадратичное отклонение:
.
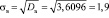Так как объём выборки невелик, то вычислим исправленное среднеквадратичное отклонение:
.
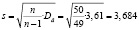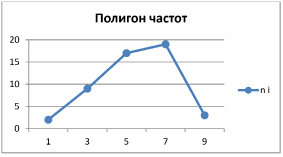
Построим полигон частот (рисунок).
По виду графика полигона частот можно заметить, что шкала надёжности распределена по нормальному закону. Найдём доверительный интервал для генеральной средней с надежностью g = 0,95. По таблице интегральной функции Лапласа Ф(t) из условия γ = 0,95 находим tγ = 1,96. Тогда точность оценки равна:
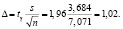
Отсюда доверительный интервал имеет вид:
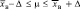или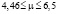 
.
Получили, что востребованными интернет-магазинами являются те, у которых оценка надёжности находится в пределах 5,6 баллов. Таким образом, покупатели делают выбор в пользу интернет-магазина со средней степенью надёжности, больше уделяя внимание цене товара.