Сетевое издание

Международный студенческий научный вестник

ISSN 2409-529X

Как показывает практика, в наше время экономисту необходима серьезная математическая подготовка. Поэтому в данной работе рассмотрим некоторые аспекты применения векторной алгебры при решении задач с экономическим содержанием. Рассмотрим некоторые теоретические вопросы, использующиеся в данной теме. При введении прямоугольной системы координат на плоскость, каждому вектору X (направленному отрезку) приводится в соответствие пара чисел, x1,x2– координат этого вектора. Это можно записать с помощью равенства X=(x1,x2). Аналогично будет и в трехмерном пространстве X=(x1,x2,x3). Подытожив факты, получим следующее определение, в котором n означает любое натуральное число. Любая последовательность из n действительных чисел x1,x2,…, xn, которые называются компонентами вектора, и есть арифметический n-мерный вектор. Обозначается n-мерный вектор: X=(x1,x2, …, xn).

Как будет видно далее, векторы очень удобно использовать для описания реальных процессов, в том числе экономических. Например, под товаром понимаются некоторый товар или услуга, поступившие в продажу в определенном месте и в определенное время.

Предположим, что имеется n различных товаров, количество i-го товара обозначается xi, тогда некоторый набор товаров обозначается X=(x1,x2, …, xn), т.е. является n – мерным вектором. Будем рассматривать, как принято, только неотрицательные количества товаров, поэтому для любого i = 1, n, xi≥ 0 или X ≥ 0. Пространство товаров – множество всех наборов товаров. Далее предположим, что каждый товар имеет цену. Все цены могут быть только положительными. Тогда вектор C=(c1, c2, …, cn) есть вектор цен, при условии, что цена единицы i-го товара есть ci. Вектор цен и вектор набора товара имеет одинаковую размерность. Для вектора цен C=(ci) и набора товаров X=(xi) их скалярное произведение 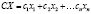есть число, называемое ценой набора товаров или его стоимостью.

Рассмотрим несколько задач с применением векторов в экономике. Пусть завод производит мужские, женские и детские ролики. Тогда объем его производства V за год можно записать как вектор V=(M, L, K), где М – объем производства за год мужских велосипедов, L – женских, K – детских. Допустим, что объем производства в 2013 г. был 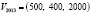. Предположим, что объем производства в 2014 г. был на 10 % больше объема производства в 2005 г., следовательно, объем производства в 2014 г. есть вектор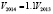 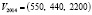. Пусть торговая фирма «Велосипеды» приобрела половину всей продукции завода, тогда в 2013 г. фирма купила W=0/5V2014, т.е. вектор закупки – W=(500, 400, 2000). Предположим, что в стране всего 2 завода по производству роликов, объемы производства которых в 2013 г. были Q1=(500, 400, 2000), Q2=(800, 1000, 4000). Тогда оба завода произвели вместе в 2013: Q=Q1 +Q2=(1300, 1400, 4000), т.е. 1300 мужских, 1400 женских и 6000 детских роликов. На данном примере – производство роликов – мы рассмотрели такие операции над векторами, как сложение векторов и умножение вектора на число.

Также можно рассмотреть следующую задачу. Коммерческий банк, участвующий в строительстве сети социальных аптек в Ставрополе, предпринял усилия по получению кредитов в 4 коммерческих банках: «Сбербанк», «ВТБ24», «Московский индустриальный банк», «Россельхозбанк». Каждый из них предоставил кредиты в размерах соответственно 10, 30,20 и 40 млрд. руб. под годовую процентную ставку25, 15,30 и 20 %. В данном случае речь идет о двух векторах: трехмерном векторе кредитов K=(10, 30, 20,40) и векторе процентных ставок P=(25, 15, 30,20). Для расчетов вместо вектора процентных ставок P удобнее использовать вектор коэффициентов P1=(1.25, 1.15, 1.3,1.2). Используя простой расчет, управляющий коммерческим банком может определить, сколь придется платить по истечении года за кредиты, взятые у банков: KP1 1.2 = 120 млрд. руб. На данном примере мы рассмотрели применение операции скалярного произведения векторов.

Очень интересным является использование элементов векторной алгебры, которую можно рассмотреть в следующей задаче. Предприятие выпускает ежесуточно четыре вида изделий, основные производственно-экономические показатели которых приведены в таблице.

Следует рассчитать следующие ежесуточные показатели: расход сырья S, затраты рабочего времени Т и стоимость Р выпускаемой продукции предприятия.

Решение. Составим четыре вектора, характеризующие весь производственный цикл по данным таблицы:

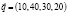– вектор ассортимента,

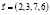– вектор расхода сырья,

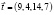– вектор затраты рабочего времени,

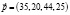– ценовой вектор.

Тогда искомые величины будут представлять собой соответствующие скалярные произведения вектора ассортимента 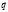на три других вектора, т. е.

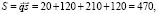
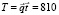ч,

.

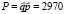Применение векторов подробно описано в следующей задаче. Побывав на Омском экспериментальном заводе сельскохозяйственной техники, были определены ежесуточны экономические показатели ОЭЗ, которые представлены в таблице.

Экономические показатели ОЭЗ

Необходимо найти цены на сельскохозяйственную технику, расходы и затраты сырья.

Решение. Для рассмотрения производственного процесса введем 4 вектора: 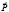– вектор расхода сырья; 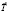– вектор времени; 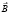– вектор изделия товара; 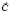– вектор цены.

В соответствии с данными таблицы получим:

; ;

;

.

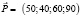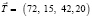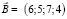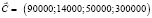Очевидно, что соответствующие скалярные произведения векторов, представляющие искомые величины, будут делиться на три других вектора:

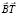=6?120+5?150+7?420+4?220=720+750+ +2940+880=5290 ч;

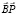=6?50+5?40+7?60+4?90=300+200+420+360==1280 кг;

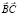=6?90000+5?14000+7?50000+4?300000= =540000+70000+ 350000+1200000= =2160000 денежных единиц.

По результатам решения можно сделать следующий вывод, что необходимо потратить сырья в размере 1280 килограмм, при этом на это потребуется 5290 часа и 2160000 денежных единиц.

Таким образом, можно сделать вывод о том, что в современной математике и ее приложениях векторы играют важную роль. Векторы так же широко применяются в теории относительности, квантовой физике, в классической механике Галилея-Ньютона (в ее современном изложении), в математической экономике и многих других разделах естествознания, не говоря уже о применении векторов в различных областях математики.