Ни для кого не секрет, что математика – фундаментальная, очень обширная наука, включающая в себя множество разделов. Так же нельзя не отметить её огромное значение в жизни каждого человека и человечества в целом. Практически все экономические и политические процессы тем или иным образом связаны с математическими расчётами, а все остальные науки хотя и в разной степени, но связаны с математикой. Одним из разделов математики является линейная алгебра, с помощью которой происходит изучение объектов линейной природы, векторных (линейных) пространств и т.д.
Первыми исследованиями в области линейной алгебры были решения системы линейных уравнений. Первым, кто уделил наибольшее внимание этой науке, был Готфрид Вильгельм Лейбниц, который в 1693 г. стал активно применять линейную алгебру на практике. В начале XX века линейная алгебра стала обязательным предметом для изучения в средних и высших образовательных учреждениях.
Что же используется в линейной алгебре? В первую очередь это решение систем линейных уравнений, составление матриц, нахождение детерминантов и изучение векторов и векторных пространств. Чтобы хоть немного вникнуть в сущность линейной алгебры, нужно знать значение основных понятий этого раздела.
Матрица – математический объект, который записывают в виде прямоугольной таблицы элементов, которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают её размер.
Система линейных уравнений – это объединение m линейных уравнений, каждое из которых содержит n переменных. Записывается в виде:
,
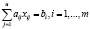Вектор – направленный отрезок, который можно перемещать в пространстве параллельно самому себе, так же вектор – это элемент некоторого непустого множества, на котором определены две операции: сложение и умножение векторов на вещественные числа.
Векторное пространство – это математическая структура, которая представляет собой множество векторов, для которых определены операции сложения векторов между собой и умножение на число. Если под множеством векторов понимать элементы любой природы, то множество называется линейным пространством.
Нельзя не отметить, что все эти понятия используются не только в линейной алгебре, но и в других сферах, например, в экономике. Так как экономический анализ практически всегда сопровождается математическими подсчётами количественных изменений, линейная алгебра неразрывно связана с ней, хотя это и две разные области знаний, которые имеют разные предметы изучений. Наиболее распространённый метод решения экономических задач – составление матриц, которые имеют широкое применение в экономических исследованиях, так как большинство реальных экономических ситуаций удобно описывать простой и компактной матричной форме.
Например: дана таблица средних розничных цен на автомобили в зависимости от срока их службы и года выпуска.
|
Продолжительность службы (годы) |
Годы выпуска автомобилей |
||
|
2011 |
2012 |
2013 |
|
|
1 |
10500 |
10820 |
11200 |
|
2 |
9320 |
9500 |
10000 |
|
3 |
7500 |
7999 |
8400 |
|
4 |
5684 |
5890 |
6300 |
Таблицу можно записать в виде матрицы следующим образом:
.
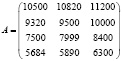Можно увидеть, что в строках отображены цены автомобилей, прослуживших одно и то же количество лет, а в столбцах – цены автомобилей, выпущенных в одно время, но эксплуатируемых разное количество времени. Таким образом можно увидеть, что каждый элемент матрицы отражает годы эксплуатации автомобиля и год его выпуска.
Применение матриц так же используется при решении экономических задач, рассмотрим это на следующем примере: Предприятие по производству сельскохозяйственной техники выпускает товары трех видов: тракторы (P1), комбайны (P2) и культиваторы (P3) и использует два типа сырья: чёрный металл (S1),и цветной металл (S2). Нормы расхода запасов металла отображены в матрице:
.
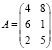где каждый элемент aij показывает, сколько единиц сырья j-го типа расходуется на производство единицы продукции i-го вида. План выпуска продукции задан матрицей-строкой C = (90 50 140). Стоимость единицы каждого типа сырья – матрицей-столбцом:
.
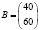Необходимо найти общую стоимость сырья. Для это нужно посчитать затраты первого сырья. Они составляют S1 = 4?90 + 6?50 + 2?140 = 940 единиц, а затраты второго:
S2 = 8?90 + 1?50 + 5?140 = 1470 единиц.
Значит, затраты сырья S могут быть записаны в виде матрицы строки S = (940 1470) и произведения:
.
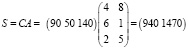Общая стоимость двух видов металла составит
Q = 940?40 + 1470?60 = 125800 (денежных единиц).
Рассмотрим ещё одну задачу:
Завоз определённых товаров на склады можно отобразить в следующих матрицах:
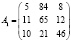– ввоз товаров на первый склад;
– ввоз товаров на второй склад;
Требуется найти сумму завоза всех товаров за год если производится ежемесячный завоз идентичных партий товара.
Найдём суммарный завоз:
.
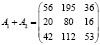Далее мы можем найти годовой завоз:
.
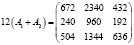Вычислив с помощью матриц годовой завоз товаров на первый и второй склады, мы смогли получить ответ.
Также можно решать экономические задачи путём составления системы линейных уравнений. Рассмотрим на примере: Предприятие выпускает три вида продукции, используя сырье трех видов. Характеристики производства, которые нужны нам для решения данной задачи, представлены в таблице.
|
Вид сырья |
Расход сырья по видам продукции, вес. ед./изд.. |
Запас сырья, вес. ед |
||
|
1 |
2 |
3 |
||
|
1 |
5 |
2 |
6 |
2470 |
|
2 |
7 |
4 |
9 |
3845 |
|
3 |
3 |
8 |
2 |
2450 |
Нужно определить объем выпуска продукции каждого вида при заданных запасах сырья.
Такие задачи используются при прогнозировании расхода сырья на производстве и определении уровня экономического функционирования предприятия.
Обозначим неизвестные объемы выпуска продукции через x1, x2 и x3. Тогда при условии полного расхода запасов каждого вида сырья можно составить соотношения, которые образуют систему трех уравнений с тремя неизвестными:
.
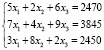Решив эту систему любым способом (Методом Гаусса, Крамара, матричным методом и т.д.), мы получим объемы выпуска продукции при заданном количестве сырья:
x1=120; x2=200; x3=245.
Экономические расчёты с использованием матриц очень удобны тем, что в них можно компактно записать множество переменных. К недостаткам можно отнести невозможность прогнозировать изменение этих переменных в будущем. Помимо матриц и матричных уравнений в экономике часто используются и векторы.
Например, можно вычислить производственные показатели предприятия, которые отображены в следующей таблице.
|
Вид изделий |
Количество изделий |
Расход сырья |
Норма времени изготовления |
Цена |
|
1 |
30 |
5 |
7 |
15 |
|
2 |
70 |
10 |
9 |
14 |
|
3 |
20 |
2 |
12 |
16 |
|
4 |
15 |
3 |
15 |
26 |
Необходимо определить следующие ежесуточные показатели: расход сырья A, затраты рабочего времени B и стоимость C выпускаемой продукции предприятия. По приведенным данным составим векторы, которые характеризуют весь производственный цикл:
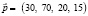– вектор ассортимента;
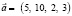– вектор расхода сырья;
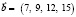– вектор затрат рабочего времени;
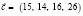– ценовой вектор.
Тогда величины, которые нам нужно найти, будут равны скалярным произведениям вектора ассортимента на три других вектора:
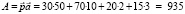кг;
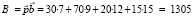ч;
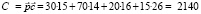ден. ед.
На примере этих задач можно наглядно увидеть, какой существенный вклад вносит линейная алгебра в изучение экономики. Нельзя переоценить пользу использования методов линейной алгебры в экономических задачах. Конечно, не все экономические процессы и изменения можно описать данным способом, но большинство расчётов существенно упрощается в результате использования матричной и векторной алгебры.