Применение экономико-математического моделирования в анализе хозяйственной деятельности позволяет достичь наиболее глубокого изучения воздействия отдельно взятых факторов на агрегированные экономические показатели деятельности предприятий, сокращения сроков осуществления анализа, повышения объективности и точности экономических расчетов. При использовании экономико-математических моделей в экономическом анализе осуществляется разработка и изучение экономико-математических показателей, которые описывают влияние отдельно взятых факторов на резюмирующие экономические показатели деятельности организаций.
Выделяют четыре основных вида экономико-математических моделей, используемых при анализе влияния отдельных факторов:
Мультипликативные модели определяются как произведение отдельных факторов, они используются, когда необходимо проанализировать воздействие различных факторов на какой-либо конечный показатель, при условии, что все факторы являются сомножителями, а полученный результат – их произведение.
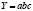 .
.
Используя данную формулу, мы можем рассчитать уровень влияния различных факторов на объемы выпускаемой продукции:
Постройте трехфакторную мультипликативную модель результативного показателя. Рассчитайте влияние факторов оптимальным с вашей точки зрения способом.
Среднегодовая стоимость основных производственных фондов, тыс. руб.:
По плану – t0=8600, по факту – 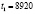 .
.
Удельный вес активной части ОПФ (k).
По плану: 0,57, по факту: 0,55
Фондоотдача активной части основных фондов, руб.
ФО по плану: 1,25, по факту ФО – 1,15
 ,
,
где ТП – объем выпущенной продукции. руб.; t – cтоимость основных фондов производства, тыс. руб.; ka – удельный вес активной части ОПФ; ФО – фондоотдача.
Рассчитаем влияние факторов на объем выпущенной товарной продукции.
Сначала найдем абсолютную разницу каждого из сомножителей:
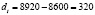 ;
;
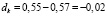 ;
;
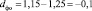 ;
;
Плановое значение товарной продукции (тыс. руб.):
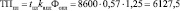 .
.
Фактическое значение товарной продукции (тыс. руб.):
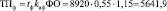 .
.
Аддитивные модели определяются как алгебраическая сумма отдельных взятых показателей. Подобные модели могут быть отражены с помощью следующей формулы:
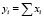 .
.
При расчете величины затрат, удобно применить данную формулу:
Рассчитайте общую величину затрат предприятия, если трудовые затраты равны 50 чел. дней, материальные затраты – 2000000 руб., а амортизация равна 50000 руб.
З=ТЗ+МЗ+АЗ,
где З – общие затраты, ТЗ – трудовые затраты, МЗ – материальные расходы, АЗ – амортизация.
Тогда, 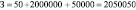 .
.
На примере данной задачи, мы увидели, как аддитивные модели применяются на практике.
Кратные модели – это соотношение отдельных факторов. Такие модели характеризуются формулой:
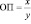 .
.
В конкретном случае ОП является обобщающим экономическим показателем, который находится под влиянием отдельных факторов x и y.
Определите продолжительность оборота оборотных активов, при условии, что средняя величина оборотных активов равна 950400 руб., а однодневный общий объем продаж – 500170 руб.
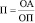 ,
,
где П – продолжительность оборота, ОА – средняя величина оборотных активов, ОП – однодневный объем продаж.
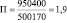 .
.
В результате использования кратной модели, мы определили однодневный общий объем продаж.
Смешанные модели – это объединение в единое целое уже рассмотренных выше видов моделей.
В обобщенном виде смешанная модель может быть представлена такой формулой:
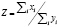 .
.
Рассмотрим данную формулу на следующем примере:
Определите показатель рентабельности активов, на уровень которого влияют чистая прибыль (ЧП) – 950000 руб., величина внеоборотных активов (ВА) – 220000 руб., а величина оборотных активов (ВА) – 370000 руб.
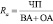 .
.
Тогда, показатель рентабельности будет равен:
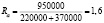 .
.
Большое распространение в анализе хозяйственной деятельности получили многофакторные мультипликативные модели, так как они дают возможность изучить воздействие значительного количества факторов на обобщающие показатели и тем самым достичь большей точности и глубины анализа.
Таким образом, под экономико-математической моделью понимают математическое описание исследуемого экономического объекта или процесса. Данная модель выражает закономерности изменения экономического процесса в абстрактном виде с помощью математических соотношений. Применение математического моделирования в экономике позволяет основательно осуществить количественный экономический анализ, увеличить область использования экономической информации.
Использование рассмотренных экономико-математических методов позволяет кардинально улучшить качество планирования и извлечь дополнительный эффект без внедрения в производство дополнительных ресурсов.

