Проанализируем методы линейных дифференциальных уравнений применяемых в исследовании различных макроэкономических моделей, где в роли независимой переменной выступает t. Эффективность данных моделей обусловлена использованием эволюции какой-либо экономической системы в длительных интервалах времени. Более того, данные системы являются предметом изучения изменения динамики в экономике.
Под экономической системой понимается совокупность хозяйственных единиц – организации и предприятии связанных между собой устойчивыми производственными связями.
Экономическая система будет являться динамической при условии наличия в этой системе так называемых динамических элементов.
Выход в любой момент времени t динамического элемента системы напрямую зависит от значений выходов и входов в случившиеся моменты времени т.е. t – 1, t – 2, и так до t – n.
Рассмотрим динамические экономические системы в качестве линейных систем при условии непрерывности времени. Таким образом, элемент динамической системы порядка n будет иметь следующий вид:
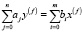. (1)
На практике лучше всего применяются элементы нулевого (к примеру мультипликатор), первого и других порядков.
Переход экономической системы из одного равновесного состояния в другое является основным элементом в исследовании динамических процессов. В случае, когда подобный переход осуществляется в течении длительного периода времени, понятие экономического равновесия утрачивает заложенный в него смысл, следовательно возникает необходимость изучения непрерывного динамического процесса преобразования экономики. Для этого в качестве инструмента может быть использована теория дифференциальных уравнений. За основу будет взята динамическая модель Кейнса.
В модели Кейнса установлено, что ВВП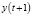 
следующего года равен валовому спросу текущего года. В свою очередь валовый спрос, включающий спрос на потребительские товары (C) и инвестиционные товары (I) напрямую зависит от ВВП текущего года т.е.:
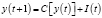. (2)
Из данной линейной зависимости спроса на потребительские товары от ВВП и постоянства спроса на товары следует соотношение:
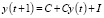, (3)
где C – это минимальный объем потребительского фонда, неизменяемый при увеличении роста национального дохода;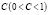 
– склонность к потреблению.
Данное соотношение действует при условии прерывности времени в один год, при прерывности ?t выражение будет иметь следующий вид
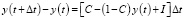, (4)
где (1–С) – склонность к накоплению.
В рамках изучения динамики наиболее эффективно использовать непрерывное время, при условии применения формальной записи модели в виде дифференциального уравнения.
Проанализируем динамику перехода национального дохода в равновесное состояние, при этом применяя модель в форме дифференциального уравнения с непрерывным временем.
В ходе преобразований при условии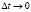 
получим следующее уравнение:
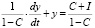. (5)
Имеется, что общим решением неоднородного дифференциального уравнения является сумма какого-либо его частного и общего решения, которые относятся к однородному дифференциальному уравнению:
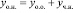(6)
Частным решением уравнения (6) будет выступать стационарное решение.
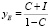. (7)
Рассмотрим следующее однородное дифференциальное уравнение:
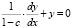. (8)
Данное уравнение с разделяющимися переменными, следовательно:
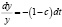. (9)
После интегрирования обеих частей этого уравнения, получается:
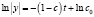, (10)
где c0>0
yo.o. =c0е–(1–с)t;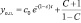 
. (11)
Изменение спроса на инвестиционные товары с I0 до I, причем I>I0, приводит к изменению значения ВВП от
,
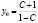до значения y=E, при этом
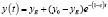. (12)
Можно сделать вывод, что при любом исходном значении y0 национального дохода, вскоре его значение становится идентичным значению в состоянии равновесия yK. Для определения скорости перехода всостоянию равновесия используют коэффициент склонности к сбережению 1–c. Чем выше этот коэффициент, тем быстрее приближается значение национального дохода к равновесному.
При условии, что в начальный период времени y0>yE, в остальные периоды значение национального дохода будет превышать равновесный за все время при постоянном уровне инвестиций.
В другом случае, при исходном y0<yE, следующие значения национального дохода будут меньше равновесного за весь временной промежуток при постоянном уровне инвестиций.
Представление экономики как линейного динамического звена второго порядка в форме модели Самуэльсона-Хикса.
Добавим к динамической модели Кейнса акселератор. Выход и вход этой категории пропорциональны. В настоящей теории экономики часто встречается такое определение: «отношение прироста индуцированных подъемом производства инвестиций к вызвавшему его относительному приросту объема производства».
Инвестиции представляются следующим выражением:
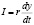, (13)
где r – коэффициент акселерации, приращение необходимости во вкладах при положительной динамике ВВП на единицу, 0 <r< 1.
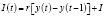, (14)
При подставлении полученного выражения в динамическую Модель Кейнса, получим:
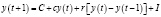, (15)
После преобразований:
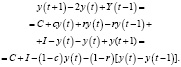(16)
Рассмотрим непрерывный интервал времени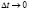 
:
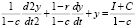. (17)
Итогом вычислений является однородное линейное уравнение второго порядка. Общее решение неоднородного уравнения предстает суммой общего однородного и частного решений неоднородного уравнения.
Общее решение линейного однородного уравнения в виде:
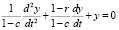. (18)
Здесь необходима замена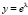 
, при которой:
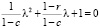. (19)
Общим решением однородного уравнения является линейная комбинация фундаментальных решени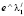й 
и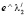 
:
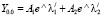. (20)
Частное решение неоднородного уравнения:
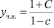. (21)
А его общее решение:
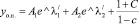. (22)
Частное стационарное решение в этом случае будет одинаковым с решением в модели Кейнса:
.
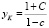Если обратить внимание на незначительные отклонения от равновесной точки, заметно, что эта система непостоянно устойчива. Описываемая моделью Самуэльсона-Хикса экономика устойчива при 0<r<1 и неустойчива при r≥1.