В экономической литературе модель Леонтьева является одной из самых известных моделей. Она подвергалась многократным улучшениям и усовершенствованиям и является основной для построения целого класса подобных моделей. В многоотраслевой экономике эта модель позволила проводить балансовый анализ, то есть отвечать на вопросы связанные с эффективностью той или иной отрасли в многоотраслевом хозяйстве страны. Каждая отрасль выступает, с одной стороны как потребитель продукции из своей, и смежных отраслей, а с другой – производитель некоторой продукции. Связи между отраслями отражаются в таблицах межотраслевого баланса.
Затраты живого трудав производстве j-го продукта обозначим через Lj, а валовой выпуск этого продукта через Xj. В этом случае коэффициент прямой трудоемкости можно записать в виде следующей формулы [1]:
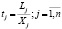. (1)
Введем представление полных затрат труда как прямых затрат живого труда и суммы затрат овеществленного труда, перенесенных на продукт при помощи израсходованных средств производства. Обозначим величину полных затрат труда на единицу продукции j-го вида через Tj. Видим, что произведения вида atjфTj отражают затраты реализованного труда, который перенесён на единицу j-го продукта через i-е средство производства [2]. При этом считаем возможным, что коэффициенты прямых материальных затрат – atj выражены в натуральных единицах. Тем временем, полные трудовые затраты на единицу j-го вида продукции будут равны [4]
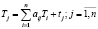. (2)
Введём вектор-строку коэффициентов полной трудоемкости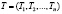 
и вектор-строку коэффициентов прямой трудоемкости 
.
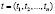Запишем матрицу коэффициентов прямых материальных затрат в матричном виде [5]:
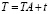. (3)
С использованием единичной матрицы E, сделаем очевидные матричные преобразования [6]
,
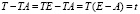для вектора коэффициентов полной трудоемкости получаем следующее соотношение:
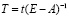. (4)
Знакомую нам матрицу (Е – А) коэффициентов полных материальных затрат, можно переписать в виде [6]
.
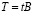Величину совокупных затрат живого труда по всем видам продукции, обозначим через L, которая с учетом формулы (1) будет равна [7]
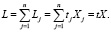(5)
Используя систему уравнений в матричной форме, соотношения (5) и (4), придём к следующему равенству:
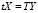. (6)
В этом случае, t и Т – вектор-строки коэффициентов полной и прямой трудоемкости, а X и Y – вектор-столбцы конечной и валовой продукции [8].
На основе коэффициентов полной и прямой трудоемкости могут быть разработаны межпродуктовые и межотраслевые балансы затрат труда и применения трудовых ресурсов. Схематически эти балансы строятся согласно общему типу матричных моделей, тем не менее все показатели в них проявлены в трудовых измерителях [9].
Пример. Требуется определить коэффициенты прямой и полной трудоемкости и составить межотраслевой баланс затрат труда. Заданы затраты живого труда в 3 отраслях: L1 = 1160, L2 = 460, L3= 875 в некоторых единицах измерения трудовых затрат.
Решение.
1. Воспользуемся формулой (1). Найдём коэффициенты прямой трудоемкости.
2. Найдём коэффициенты полной трудоемкости по формуле (4), в которой в качестве матрицы Вберется матрица коэффициента полных материальных затрат.
|
Производящие отрасли |
Потребляющие отрасли |
||||
|
Межотраслевые затраты овеществленного труда |
Затратытруда на конечную продукцию |
Затраты труда в отраслях (трудовые ресурсы) |
|||
|
1 |
2 |
3 |
|||
|
1 |
348,9 |
76,5 |
437,7 |
300,0 |
1163,0 |
|
2 |
139,6 |
229,5 |
0,0 |
90,0 |
459,1 |
|
3 |
279,1 |
61,2 |
175,1 |
360,0 |
875,5 |
3. Умножая третью, вторую и первую строки первого и второго квадрантов межотраслевого материального баланса, соответствующие им коэффициенты прямой трудоемкости, получим схему межотраслевого баланса труда (таблица).
Расхождения между данными таблицы и исходными данными, которые мы замечаем, вызваны погрешностями округления при вычислениях [10].
Развитие основной модели межотраслевого балансаможетдостигается путем включения в нее показателей фондоёмкости продукции. В элементарном случае данная модель будет дополняться отдельной строкой, в которой будут указаны объемы производственных фондов Фj в стоимостном выражении, занятые в каждой отрасли [11].
Определяя коэффициенты прямой фондоёмкости продукции j-го отрасли, возьмём во внимание объемы валовой продукции всех отраслей и все данные из таблицы. Получим:
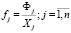. (7)
Коэффициент прямой фондоёмкости будет указывать величину производственных фондов, которые занимаются в производстве данной отрасли, в расчете на единицу валовой продукции [12]. В отличие от коэффициента прямой фондоёмкости, коэффициент полной фондоёмкости Fj отражает объем фондов, которые необходимы для выпуска единицы конечной продукции j-й отрасли, во всех секторах экономики. Если aij – коэффициент прямых материальных затрат, то для коэффициента полной фондоемкости будет справедливо равенство, которое аналогично неравенству (2) для коэффициента полной трудоемкости [10]
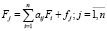. (8)
Если мы введём вектор-строку коэффициентов прямой фондоёмкости
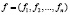
и вектор-строку коэффициентов полной фондоёмкости
,
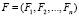то систему уравнений (8) можно будет переписать в матричной форме:
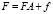. (9)
Откуда, используя преобразования, аналогичные применяемым выше для коэффициентов трудоемкости, можно получить матричное соотношение
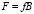, (10)
где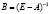 
– матрица коэффициентов полных материальных затрат.
Коэффициенты фондоёмкости в межотраслевом балансе позволяют увязать планируемый выпуск продукции с имеющимися производственными мощностями.