Дискретная математика или дискретный анализ – направление в математике, соединяющее отдельные ее сегменты, ранее сформировавшиеся как самостоятельные теории. К ним можно отнести математическую логику и теорию множеств, графов, кодирования, автоматов. Дискретная математика исследует объекты, чаще всего не имеющие ни физической, ни числовой интерпретации. В классической математике закономерности можно представить соотношений, а характеристики реальных объектов можно представить в виде чисел. В отличие от настоящих характеристик информационных объектов могут послужить такие понятия, как «структура», «отношение», «связь». Чаще всего объекты информатики рассматриваются в виде некоторых знаков, над которыми можно произвести различные операции.
В данное время в обществе возникают разногласия, не позволяющие методами классической высшей математики моделировать интеллектуальные и кибернетические системы. Следовательно, появилась дискретная математика, которая работает для описания основных систем информационного периода. Дискретная математика является основой проектирования цифровых электронных устройств. Первое применениедискретной математики в данной области будут связаны с именами К.Э. Шеннона, В.А. Котельникова, В.И. Шестакова. Появление математической теории управляющих систем приводит к развитию более новых разделов дискретной математики, таких как: теория сложности, теория надежности схем, теория автоматов и многих других. Большой вклад в дискретную математику сделали С.В. Яблонский, Дж. фон Нейман, А.А. Ляпунов, О.Б. Лупанов.
В экономике присутствует огромное количество отраслей, использующие способы дискретной математики. К ним можно отнести эконометрику, логистику, и математическое моделирование. Таким способом, в эконометрике булевские переменные применяют в исследовании регрессионной модели с переменными структурами и в построениях регрессионной модели по неоднородным данным. В таком случае мы рассматриваемтолько единственное уравнение регрессии, куда вводят булевые переменные, характеризуемые факторы подлежащие изменениям. Этот способ благоприятен для того, чтобы выявить зависимость модели от различных факторов. Теория графов обширно применяется в логистике для описания потоков, задания маршрутов. Например, схему дорог будет удобнопредложить в виде ориентированного графа, и известными нам способами мы сможем выбрать наиболее короткую дорогу. В наше время, прокладывая маршрут, надо брать и пропускную способность магистралей, интерпретируя маршруты в графы, возможно, получать экономически выгодные решения.С помощью теории нечетких множеств, методом нечеткого предпочтения, мы выбираем конкурентоспособный продукт или услугу. Поэтому данная теория используется в маркетологии, при исследовании рынка всевозможных финансовых благ.
Нам дана задача. Расстояние между городами Буденовском и Георгиевском 6 км, между Буденовском и Ессентуки – 7 км, между Буденовском и Железноводском – 20 км, между Буденовском и Кисловодском – 12 км, между Буденовском и Пятигорском – 10 км. Расстояние между Георгиевском и Ессентуками составляет 5 км, между Георгиевском и Железноводском – 7 км, между Георгиевском и Кисловодском – 9 км, между Георгиевском и Пятигорском – 16 км. Расстояние между Ессентуками и Железноводском – 4 км, между Ессентуками и Кисловодском – 10 км, между Ессентуками и Пятигорском – 12 км. Расстояние между Железноводском и Кисловодском 3 км, между Железноводском и Пятигорском расстояние в 15 км. Расстояние между Кисловодском и Пятигорском будет составлять 6 км, между Кисловодском и Пятигорском – 4 км, между Пятигорском и Ессентуками- 11 км, между Пятигорском иКисловодском – 21 км. Так как Николаю надопобывать во всех 6 городах по одному разу, возвратиться в начальный пункт, тонужно найти маршрут, при котором расстояние в сумме будет минимальным.
Эту задачу можно решить венгерским способом, способом совершенного пар о сочетания.
 .
.
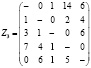
Составленная матрица Z будет отображать расстояние между городами, где Zij – дистанция между городом i и городом j (i ≠j), в случае i = j поставим – так как дорога не будет существовать.
Данная матрица построена с целью получения в каждой строке и столбце не менее одного наиболее краткого пути. Для этого в каждой строке матрицы Z от каждого элемента будет отниматься минимальное значение элемента данной строки:
 .
.
Вычисляем коэффициент приведения, который равен сумме всех минимальных элементов матрицы Z, вычитаемые из строк и столбцов:
Коэффициент приведения равен
6+5+4+3+4+10=32.
Рассчитываются коэффициенты значимости для каждого занулившегося элемента, где Zij – элементы приведенной матрицы.
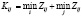 .
.
Коэффициенты значимости примут значения:
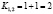 ,
, 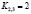 ,
, 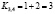 ,
,
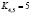 ,
, 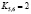 ,
, 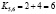 .
.
Из данной матрицы нам нужно убрать строку и столбец, содержащий элемент с максимальным коэффициентом значимости. В этом случае этим элементом будет являться Z=5,6: коэффициент значимости равен 6. Для элемента Z=5,6 установим значение 1, то есть 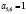 .
.
 .
.
Коэффициенты значимости:
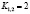 ,
, 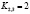 ,
, 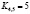 ,
, 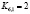 ,
,
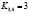 ,
, 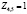 .
.
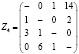 .
.
Коэффициент значимости:
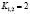 ,
, 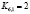 ,
, 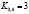 ,
, 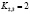 ,
, 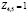 .
.
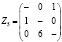
Коэффициент значимости:
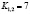 ,
,  ,
, 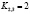 ,
, 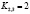 ,
, 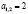 ,
,
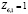 ,
, 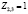 .
.
Таким образом, в маршрут вошли ребра: {Кисловодск, Пятигорск}, {Железноводск, Кисловодск}, {Ессентуки, Железноводск}, {Буденновск, Георгиевск}, {Пятигорск, Буденновск}, {Георгиевск, Ессентуки}. Все городаобъединились.
Протяженность составляет w({Кисловодск, Пятигорск}) + w({Железноводск, Кисловодск}) + w({Ессентуки, Железноводск}) +w({Буденновск, Георгиевск}) + w({Георгиевск, Ессентуки}) = 4 + 3 + 4 + +6 + 10 + 5 = 32.
Дорога Николая пройдёт по следующему маршруту: {Буденновск, Георгиевск}, {Георгиевск, Ессентуки}, {Ессентуки, Железноводск}, {Железноводск, Кисловодск}, {Кисловодск, Пятигорск}, {Пятигорск, Буденновск}, и с возвращением домой в Буденновск составит 32+ 10=42 км.

