Понятие предела несомненно занимает ключевое место в математике. Оно является основным понятием математического анализа, без которого невозможны многие экономические расчеты. Представление о понятии предела является очень древним, основанным на эмпирических исследованиях, а современная теория – результат систематизации и эволюции этих представлений. Такие математики древности, как Евклид и Аристотель, выдвигали идею существования предела. Но лишь спустя несколько столетий Ньютон обратил внимание на эту идею и ввел термин limes (предел).
Определение предела последовательности
Число a называется пределом последовательности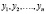 
, если по мере возрастания номера n член yn неограниченно приближается к a:
.
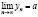Теория пределов часто используется в различных экономических вычислениях, например, в подсчитывании сложных процентов.
В основном практических расчетах применяют дискретные проценты (начисляемые с определённой периодичностью). Время – дискретная переменная. В некоторых случаях возникает необходимость в применении непрерывных процентов (например, в доказательствах расчётов, в которых происходят непрерывные процессы). Рассмотрим формулу сложных процентов
,
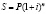где P – первоначальная сумма; i – ставка процентов (десятичная дробь); S – сумма, которая образовалась к концу срока ссуды в конце n-го года.
Пример. Найти прибыль от 30000 долларов, положенных на депозит на 3 года под 10 % годовых, если в конце каждого года проценты добавлялись к депозитному вкладу.
Решение. Используем формулу для вычисления сложных процентов:
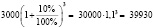долл.
В данном случае прибыль будет равна:
39930 – 30000 = 9930 долл.
Ответ: 9930 долл.
Зачастую в финансовой практике возникают задачи, обратные определению наращенной суммы: по заданной сумме, которую следует уплатить через некоторое время, необходимо определить сумму полученной ссуды. Имеем:
,
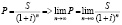где S – заданная сумма; n – время; P – полученная ссуда.
Следовательно, при очень больших сроках платежа сумма последнего будет крайне незначительна. В финансово-кредитных операциях непрерывные процессы наращения денежных сумм почти не используются, однако при выборе и обосновании инвестиционных решений они необходимы (многие экономические явления по своей природе непрерывны). Разновидность формулы сложных процентов в случае, когда проценты начисляются m раз в году:
,
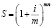где m – число периодов начисления в году, i – годовая ставка.
Логично, что чем больше m, тем меньше n между моментами начисления процентов. В пределе при m →∞ имеем:
.
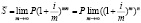Так как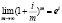 
, то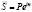 
.
Чтобы было возможно отличать ставки непрерывных и дискретных процентов, непрерывную ставку обозначим d, тогда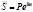 
.
Пределы так же применяются при использовании производной в экономике. Если функция u=u(t) – объем произведенной продукции за время t, то производная u›(t0) есть производительность труда в момент времени t0. Если y=f(x) – издержки производства при производстве xединиц продукции, то производная y›=f›(x0) выражает предельные издержки производства и характеризует приближенно дополнительные затраты на производство дополнительной продукции. Также существуют другие величины, характеризующие предельные процессы выручки, дохода, продукта, полезности, производительность и т.д.
Если предельные издержки и цена продукции равны, то в таких случаях говорят, что выпуск продукции является оптимальным для производителя.
,
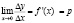где ?y – изменение денежных единиц, ?x – изменение выпуска продукции, p – цена продукции.
Рассмотрим соотношение между предельным и средним доходами. Пусть p – цена, а q–количество продукции, тогда r = pq, где r – суммарный доход.
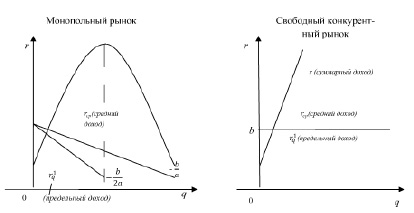
Рассмотрим монопольный рынок (на цену влияет одна фирма (иногда несколько): пусть p=aq+b – кривая спроса, тогда r=(aq+b) q=aq2+bq – суммарный доход,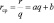 
– средний доход, 
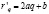– предельный доход. В таких условиях действует следующая закономерность: чем большее количество продукции продано, тем предельный доход ниже, а значит и средний доход уменьшается.
В условиях свободного конкурентного рынка товары продают по фиксированной цене (p=b), тогда r = bq – суммарный доход,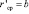 
– предельный доход, 
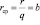– средний доход. Значит, при совершенной конкуренции предельный и средний доходы совпадают.
От 0 до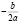 
эластичный спрос, от 
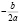до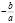 
– неэластичный спрос.
Эластичностью функции Ex(y) называется предел отношения относительного приращения функции y к относительному приращению переменной x при ?x→0:
.
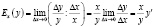Эластичность функции приближенно показывает, на сколько процентов изменится функция y = f(x) при изменении переменной x на 1 % (другими словами, эластичность показывает, на сколько процентов в среднем произойдет изменение спроса при изменении цены на 1 %). Если модуль найденной эластичности больше единицы, то спрос эластичный (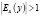
); если меньше либо равен единице, тогда спрос называют неэластичным (
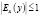); если равен единице, то говорят о спросе с единичной эластичностью 
.
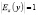При p = p(q) – произвольной кривой спроса, предельный доход (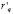
) равен:
= 
,
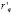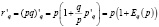или иначе
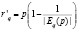так как Ep(q) < 0.
C возрастанием цены р суммарный доход от продажи продукции увеличивается (при эластичном спросе (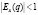
, то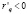 
)) или уменьшается (при неэластичном спросе (
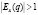, то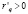 
)).
Пример: даны функции спроса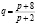 
и предложения s = p + 0,5, где p – цена товара, q – количество покупаемого товара (спрос), а s – количество предлагаемого товара (предложение). Найти рыночную цену и эластичность спроса и предложения для этой цены.
Решение. Рыночную цену найдем с помощью равенства q иs:
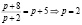(ден. ед.).
Эластичность спроса и предложения найдем по формуле
–
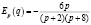эластичность спроса,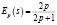 
– эластичность предложения.
Т.к. p = 2, то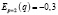 
, а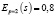 
. Значит, спрос и предложение на этот товар при рыночной цене являются неэластичными: при увеличении цены на 1 % спрос уменьшится на 0,3 %, а предложение возрастет на 0,8 %.
В ходе работы показана актуальность теории пределов при нахождении показателей в различных экономических ситуациях. Следовательно, теория пределов играет важную роль не только в математике, но и в экономике.