Балансовый анализ преследует цель увеличения эффективности ведения многоотраслевого хозяйства, отвечает на вопрос, какой объем продукции должна производить каждая из n отраслей, чтобы этот объем удовлетворял все потребности в производимой продукции. В макроэкономике это достаточно сложная проблема, если учитывать тот факт, что каждая отрасль выступает и в роли производителя, и в роли потребителя продукции, произведенной и в своей отрасли, и в других отраслях. Для решения этой задачи существуют таблицы межотраслевого баланса. И только в 1936 году Василием Васильевичем Леонтьевым, знаменитым американским экономистом, была создана математическая модель, позволяющая анализировать эти таблицы, – модель многоотраслевой экономики.
Допустим, что рассматривается конечное количество n отраслей, и каждая производит свой определенный товар. Часть произведенного идет на удовлетворение внутренних потребностей отрасли и внутрипроизводственного потребления другими отраслями, а часть – на личное и общественное потребление вне производственной сферы.
Пусть xi– это валовой (общий) объем продукции, производимый i-й отраслью, xij– это объем продукции, произведенной i-й отраслью и потребляемой j-й отраслью при производстве продукции объемом xj, а yi – это объем продукции, произведенной i-й отраслью для непроизводственного потребления (продукт конечного потребления).
Так, балансовый принцип связи отраслей производства заключается в том, что количество продукции, произведенной i-й отраслью, должно быть равно количеству продукции, потребляемой в производственной и непроизводственной сферах в сумме.Из-за этого уравнение соотношения баланса в форме простого сложения (гипотеза линейности) выглядит так:
xi= xi1+ xi2+ … + xin+ yi,
где i = 1,2, …, n
Далее Леонтьев замечает, что отношение xij к xj меняется мало из-за того, что технология производства не меняется, то есть отношение потребляемого j-й отраслью объема продукции в процессе производства к объему произведенной ею продукции является технологической константой, обозначаемой aij и называемой коэффициентом прямых затрат:
,
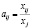где i, j = 1, 2, …,n.
Следовательно: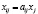 
, где i, j = 1, 2, …, n.
Тогда это уравнение мы можем записать в виде системы уравнений для n конечного количества отраслей:
.
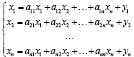Введем к рассмотрению матрицы, где X – вектор валового (общего) производства, Y – вектор конечного потребления, а A – матрица прямых затрат:
.
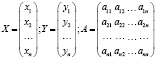Тогда система уравнений принимает вид:
X = AX + Y;
Y = (E – A)X;
X = (E – A)-1 Y = SY.
где S – матрица полных затрат, а sij – объем валового (общего) производства i-ой отраслью, необходимый для производства единицы конечного продукта j-й отрасли.
И тогда цель межотраслевого баланса заключается в нахождении вектора валового (общего) производства X при известных постоянных значениях прямых затрат A и определенном необходимом векторе конечного потребления Y.
Но модель Леонтьева считается продуктивной только тогда, когда матрица A является продуктивной. Матрица Aявляется продуктивнойтогда и только тогда, когда матрица S существует и ее элементы неотрицательны. Также матрица A считается продуктивной, если все ее элементы неотрицательны и сумма элементов любого ее ряда не превышает 1.
Рассмотрим модель Леонтьева на простом примере, где n=2 (две отрасли производства). В таблице приведены данные.
|
Отрасль |
Потребляющие отрасли |
Конечный продукт |
Валовый (общий) выпуск |
|
|
Энергетика |
Машиностроение |
|||
|
Энергетика |
3 |
8 |
89 |
100 |
|
Машиностроение |
5 |
7 |
88 |
100 |
Из данных таблицы следует:
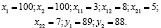
По формуле находим коэффициенты прямых затрат и составляем матрицу A:
.
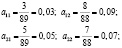
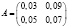Заметим, что матрица A является продуктивной. Далее найдем матрицу полных затрат:
;
;
.
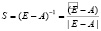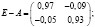
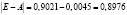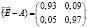Следовательно,
.
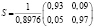Зная по условию вектор Y конечного продукта, найдем вектор X валового (общего) производства
;
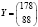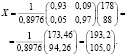
Мы получили результат, согласно которому производство в энергетической отрасли нужно увеличить до 193,2 условных единиц, а в машиностроительной – до 105 условных единиц.