Сетевое издание

Международный студенческий научный вестник

ISSN 2409-529X

Мы задались вопросом о возможности использования методов и инструментария математической статистики и теории вероятностей в экономической сфере.

Студенты экономических специальностей при изучении дисциплины «теория вероятностей и математическая статистика» нередко задаются вопросом о возможности использования полученных знаний в реальной жизни и их предстоящей деятельности. Одним из важнейших инструментов эконометрических исследований являются методы математической статистики. Это обусловлено тем, что подавляющее большинство микро- и макроэкономических показателей носит характер случайных величин, предсказание точных значений которых почти не представляется вероятным. Связи между этими параметрами обычно не носят строгий функциональный характер, а допускают присутствие случайных отклонений. Вследствие этого использование аппарата математической статистики в экономике имеет естественный характер. Теория вероятностей – основа вероятностно-статистических методов принятия решений в управлении. Чтобы получить возможность использовать в них математический аппарат, нужно задачи принятия решений выразить в терминах вероятностно-статистических моделей. Применение конкретного вероятностно-статистического метода принятия решений состоит из трех этапов:

– переход от экономических, управленческих и технологических реалий к абстрактной математико-статистической схеме, т.е. создание вероятностной модели управления, технологического процесса, порядка принятия решений, в частности по результатам контроля, основанного на статистических данных.

– проведение расчетов и получение выводов математическими методами в рамках вероятностной модели;

– представление полученных ранее выводов применительно к имеющейся ситуации. Принятие соответствующего решения (например, о соответствии или несоответствии качества продукции и услуг имеющимся стандартам, потребности в корректировке технологического процесса и т.п.), в частности, заключения (о доле единиц продукции в партии, не соответствующих требованиям; о конкретном виде законов распределения контролируемых параметров технологического процесса и др.).

Математическая статистика является практической стороной теории вероятности. Рассмотрим главные вопросы построения вероятностных моделей принятия решений в экономике. Для того чтобы правильно использовать нормативно-технических и методических документов по вероятностно-статистическим методам принятия решений требуется определенная база знаний. А именно: следует знать, при каких условиях следует применять тот или иной документ, какие решения следует принять по результатам обработки имеющихся данных и т.д.

Лишь те инструменты математической статистики, которые опираются на вероятностные модели соответствующих реальных явлений и процессов, могут использоваться для доказательства теорий. Речь идет о моделях потребительского поведения, возможности появления рисков, функционирования технологического оборудования, получения результатов эксперимента и т.п. Вероятностную модель реального явления следует считать построенной, если рассматриваемые величины и связи между ними выражены в терминах теории вероятностей. Соответствие вероятностной модели реальности обосновывают с помощью статистических методов проверки гипотез.

Невероятностные методы обработки данных являются теоретическими, их можно применять лишь при предварительном анализе данных, так как они не дают возможности оценить точность и надежность выводов, полученных на основании ограниченных статистических данных.

Вероятностно-статистические методы можно применить везде, где представляется возможным построить и обосновать вероятностную модель рассматриваемого события или процесса. Их использованием обязательно, когда сделанные на основе выборочных данных выводы переносятся на всю совокупность (например, с выборки на всю партию продукции).

Для того, чтобы нагляднее рассмотреть применение теории вероятностей в экономике, рассмотрим примеры, когда вероятностно-статистические модели являются хорошим способом решения экономических проблем.

Но все это лишь теория, а нам хотелось бы рассмотреть использование методов теории вероятностей и математической статистики на конкретном примере, напрямую связанном с предстоящей деятельностью будущих выпускников-экономистов направления «финансы и кредит».

Рассмотрим пример. Пусть банк выдает кредит в 5 млн руб. сроком на 5 лет. Вероятность невозврата кредита примем равной 5 %. Какую процентную ставку необходимо установить банку, чтобы в получить прибыль, не меньше минимальной?

Обозначим ставку, измеряемую в долях от единицы через p. Прибыль банка является величиной случайной, так как кредит вместе с процентами клиентом может быть возвращен, а может и нет. Закон распределения этой случайной величины следующий:

p=0,95; q=0,05.

Вероятность возврата кредита – 0,95. Оставшиеся 0,05 – это риск того, что кредит не будет возвращен, а банк понесет потери в сумме 5 млн.руб. Для того, чтобы узнать, какую ставку k процента нужно установить, составим неравенство:

PC(1+0,01k) – (1 – p)C≥0,

Откуда

P(1+0,01k+1) – 1≥0,

2+0,01k≥1/P;

k≥( – 2+1/P)×100;

k≥200(p – 1)/p ≈10,53.

То есть, банк должен установить процентную ставку k не меньше 10,53 % для того, чтобы свести риски к минимуму.

Инструменты математической статистики применяются не только при кредитовании, но и при страховании. Как известно, наступление страхового случая является случайным событием. Только используя математическую статистику можно провести зависимость между величиной страхового взноса и вероятностью наступления страхового случая. Рассмотрим следующий пример.

Можно в качестве примера привести работу страховых компаний. Пусть страховая компания заключает договоры страхования на один год на сумму L руб. Известно, что страховой случай произойдет с вероятностью p и не произойдет с вероятностью 1 – p = q. Составим закон распределения индикативной случайной величины Х.

Таблица 1

Здесь, х=1 – наступление страхового случая с вероятностью p; х=0 – ситуация, когда страховой случай не наступил, с вероятностью q.

Xi – количество наступивших страховых случаев у i-го страхователя. Обозначим через n количество клиентов, с которыми страховая компания заключила договор.

Таким образом, MXi = p, DXi= 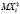– (MXi)2 = pq. Значит, MX = np и DX = npq. Из этого следует, что величина X распределена по биномиальному закону. Компания при наступлении страховых случаев обязана будет выплатить страховые возмещения в сумме npL рублей. Для того, чтобы баланс страховой компании оказался хотя бы нулевым, необходимо с каждого получить первоначальный взнос по pL рублей (т.е. 100p % от L). Но величина страховых возмещений может быть как больше страховых взносов, так и меньше. В первом случае компания останется в убытке, во втором – получит прибыль. Для того, чтобы обезопасить себя, компаниям нужно установить сумму первоначального взноса чуть большей, чем рассчитано. Тогда, пусть 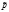– реальная ставка процента, с условием, что 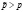. Следовательно, компания берет с n клиентов не npL руб., а 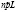руб. Эта сумма предназначена для того, чтобы покрыть убытки от наступления страхового случая у 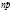страхователей. Пусть γ – вероятность того, что страховая компания не получит потерь. В этом случае вероятность наступления не более, чем 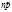страховых случаев будет равна .

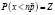Имеем

где Ф – это функция Лапласа. Теперь мы можем определить реальную страховую ставку 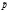. Пусть γ = 0,99 (т.е. страховая компания не разорится с вероятностью 99 %), р= 0,01 и число клиентов n = 1000. При помощи таблицы значений функции Лапласа имеем, что

.

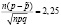Отсюда следует, что 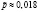. Таким же способом можно определить оптимальный размер инвестиций, результат которых без статистических исследований вычислить невозможно.

Можно объединить вышеизложенные примеры. Известно, что для того, чтобы избежать убытков, банки при выдаче кредитов приобретают страховые полисы. Как же применить математическую статистику в этом случае?

Пусть банк выдает кредиты по 3 млн руб. под 15 % сроком на год. Вероятность того, что кредит не будет возвращен, равна 0,03. Чтобы снизить риски банк покупает страховой полис на каждый из кредитов на L млн. руб., выдавая страховой компании страховую премию в 4 %. Оценить среднюю прибыль банка с одного кредита, если L=3 (если страховой полис выдан на 3 млн руб.) Обозначим величину

D = –0,04 S + X,

где 0,04 L – суммы, выплачиваемые банком страховой компании; X – случайная величина – сумма доходов и убытков кредитующей организации, закон распределения которой выглядит так.

Таблица 2

Из этого следует, что

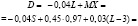
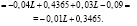
То есть, при приобретении банком страхового полиса на сумму 3 млн. рублей, прибыль банка составит 0,3165 млн. рублей.

Таким образом, мы выяснили, что аппарат теории вероятностей и математической статистики широко используется во всех областях экономической сферы и является незаменимым средством достижения наибольшей эффективности экономики в целом.