Уравнение, носящее имя нашего соотечественника Е. Слуцкого, известно в науке начиная с первой половины XX в. Оно состоит в том, что изменение спроса на некоторый товар при повышении или снижении его цены складывается из влияния непосредственного изменения спроса и косвенного влияния в результате переключения спроса на другие товары при условии неизменности уровня благосостояния. Данное уравнение показывает, что изменение в спросе на i-й товар при изменении цены j-го товара является результатом двух эффектов: эффекта замещения и эффекта дохода. Эффект замещения иногда называют изменением компенсированного спроса [1]. Идея состоит в том, что потребителю компенсируют повышение цены таким увеличением его дохода, которое позволяет ему купить старый потребительский набор. Разумеется, если цена снижается, то «компенсация» заключается в том, что у него отбирают часть денежного дохода [2].
Уравнение Слуцкого описывает поведение точки спроса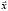 
при компенсации, когда изменения вектора цен 
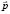и размера бюджета (дохода) q согласованы таким образом, что значение функции полезности 
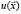(далее ФП) остается постоянным. В точке спроса выполняются стандартные условия достижения максимума ФП [3]
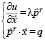(1)
где l – множитель Ланграджа, в данном случае натуральная предельная стоимость денег.
Точка спроса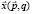 
есть однородная функция нулевого порядка, и, следовательно, она подчиняется уравнению Эйлера [4]:
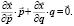(2)
Так как по условию u=const, то
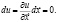
А следовательно, согласно первому уравнению системы (1):
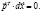(3)
Изменение точки спроса при компенсации (compensation):
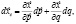
где согласно (3) приращение дохода равно:
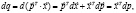(4)
т.е.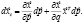 
Откуда следует классический вид уравнения Слуцкого [10]:
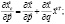(5)
(
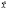– столбец; 
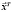– строка).
Для дальнейшего исследования целесообразно ввести диагональные матрицы P и X:
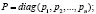
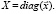
Они позволяют находить матрицу эластичности спроса e и вектор эластичности спроса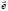 
:
;
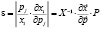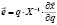. (6)
Непосредственно из уравнений (6) следует [11]:
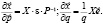(7)
Умножив обе части уравнения (5) на X–1 слева и на P справа, получим уравнение Слуцкого, выраженное в терминах эластичности [6]:
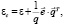(8)
где e, εc – соответственно матрицы эластичности без компенсации и при ее наличии;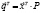 
– вектор расходов.
Введем вектор распределения относительных расходов:
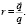
Тогда уравнение Слуцкого (8) можно записать максимально простым образом [7]
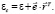(9)
Введем векторы относительных изменений спроса:
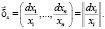
Аналогично запишем вектор относительных изменений цен
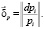
При малых величинах этих двух векторов с достаточной точностью можно считать, что они линейно зависят друг от друга
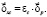(10)
Теперь предположим, что ФП – однородная функция порядка a.
Известно, что в этом случае выполняется равенство:
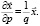
Поэтому уравнение Слуцкого (5) в случае произвольной однородной ФП приобретает вид [8]
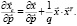(11)
Умножив каждую сторону уравнения (11) на X–1 слева и на P справа, получим соответствующее уравнение для эластичностей:
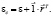(12)
Рассмотрим частный случай, когда однородная ФП является функцией Кобба-Дугласа. Тогда, как рассмотрено выше, спрос оказывается равным:
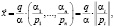
отсюда
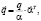(13)
где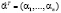 
– вектор степеней.
Далее: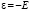 
(E единичная матрица) – эластичность без компенсации.
Отсюда следует выражение для эластичности при наличии компенсации
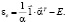(14)
Рассмотрим пример с тремя видами товара.
Задается вектор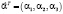 
функции Кобба-Дугласа. Задается вектор относительных изменений цен 
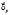(в процентах).
Требуется найти вектор относительных изменений вектора потребления при компенсации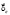 
(в процентах).
Пусть, например, векторы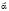 
и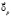 
равны:
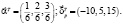
Матрица эластичности спроса при компенсации в общем случае равна:
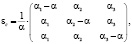
где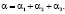 
В данном примере сумма степеней
–
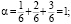
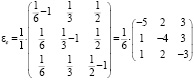матрица эластичности.
Отсюда в соответствии с равенством (10) получаем вектор относительных изменений вектора потребления:
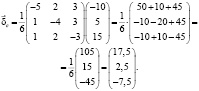
Можно видеть, что спрос на первый и второй виды товара возрос соответственно на 17,5 и на 2,5 %, а спрос на третий вид товара снизился на 7,5 %.
Нетрудно заметить, что равенство (10) позволяет решать и обратную задачу: задавшись желаемым относительным изменением спроса, определить, каким образом для этого необходимо изменить цены:
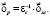
Таким образом, построена модель, в рамках которой определяется относительное изменение вектора спроса при компенсации. Одновременно решается и обратная задача на определение компенсированных изменений цен.
Показывается, что привлечение понятия эластичности спроса упрощает запись уравнения Слуцкого и его решение. Доказывается, что знание матрицы эластичности и вектора относительных расходов достаточно для определения реакции спроса для любых сравнительно небольших компенсированных изменений цен. Разумеется, если имеется информация о функции полезности потребителя, то упомянутые матрица эластичности ec и распределение расходов 
в принципе теоретически всегда можно вычислить.