Автоматизированное анализ рукописных текстов востребован в разных сферах деятельности человека. Существует не малое количество различных исследований в этой области, направленных на решение этой задачи. В свой статье я приводу пример математической модели дешифровки исторических рукописных документов, которая лежит в основе многих разработок. Распознавание различных текстов проводится на базе полученной информации о символе, а также оперяясь на информацию, полученную из текстов самого автора.
Обозначим через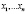 
последовательность рукописных символов. Довольно часто рукописные символы распознаются неоднозначно. Для символа xk обозначим через 
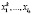множество его возможных распознаваний. Каждому опознанному символу 
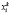определяются его возможные трактовки 
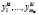. Тогда распознанный текст примет вид 
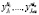. Нужно вычислить такой набор индексов, чтобы вероятность верного распознавания была максимальной.
,
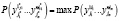где максимум берется по всем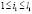 
, 
..., 
.
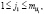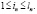
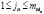Используя формулы умножения вероятностей, она равна:
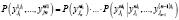. (1)
Оценим вероятность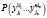 
. Оценка сомножителя формулы (1) при 
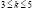выглядит таким образом:
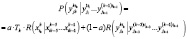. (2)
Для k<3, оценка вероятности облегчается. Полученное уравнение представляет собой обыкновенное дифференциальное нелинейное уравнение второго порядка. Оно может быть решено при помощи численных методов. Однако встроенные функции решения дифференциальных уравнений, входящие в такие общеизвестные математические пакеты программ как MatCAD, MatLAB и Maple, не позволяют решать уравнения данного типа, а возможности программирования, например в MatCAD, достаточно ограничены. Первое слагаемое формулы (2) просчитывает точность опознания рукописного символа. Второе слагаемое формулы (2) просчитывает насколько данный фрагмент текста, принадлежит данному автору. Коэффициент a определяется в зависимости от качества данного рукописного текста.
Задача первого слагаемого формулы (2) заключается в расчете точности распознавания символа данного рукописного текста. Точность распознавания символа рассчитывается по формуле
,
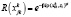где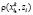 
– интервал между текущем символом и эталонном zi класса. Т.е. среди всех классов символов, используемых при записи этих рукописных текстов, нужно найти те, интервал между которыми минимален. Для вычисления данного интервала необходимо знать коэффициенты βi и γi, которые определяются исходя из системы уравнений 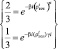(3)
, (3)
где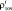 
– интервал, при котором возникает первое вхождение символа не схожего с текущим, 
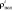– интервал, при котором вошли все символы из этого класса, схожие с текущим. При данном значении высоты капли ее форма, в отсутствие внешнего магнитного поля, может считаться равновесной, при дальнейшем увеличении высоты капли, баланс сил действующих на каплю резко нарушается, что выражается в быстром изменении ее формы и отрыве верхней части капли.
Для дальнейших вычислений используется словарь программной системы Smalt. В базе данных, которой находится порядка ста тысяч слов.