Экономическая наука в значительной степени связана с количеством товаров или факторов производства и их ценами. Факторы производства и товары продаются и покупаются на рынках. Рассмотрим рынок какого-либо определенного товара или фактора производства и одно агрегирование, то есть объединение продавцов в одну группу и покупателей в другую. Данный вид агрегирования определяет проблемы оценки, а также суммирования произведений количеств на цены.
Паутинообразная модель представляет собой простую динамическую модель, которая характеризуется затуханием колебания, итогом которого является получение равновесия.
Допустим, рынок какого-либо определенного товара характеризуется данными функциями спроса и предложения:
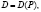
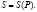
Для того чтобы поддерживать существование равновесия, цена должна быть такой, чтобы рассматриваемый товар на рынке был распродан, то есть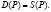 
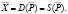
Динамическая модель образуется при отставании предложения или спроса. Простейшая модель в дискретном анализе содержит отставание или неизменное запаздывание на один интервал:
Dt=D(Pt) и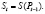 
Это может произойти в том случае, если для изготовления рассматриваемого товара необходим конкретный период времени, взятый за интервал. Действие модели таково, что при данном Pt–1 предыдущего периода величина предложения на рынке в текущем периоде будет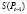 
, и объем Pt должен быть такой, чтобы был распродан весь объем предложенного товара. Таким образом, Pt и величина продаж и покупок Xt задается уравнением
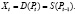
Таким образом, имея исходную цену P0, посредством заданных уравнений мы можем приобрести значения P1 и X1. Далее, используя существующую цену P1, из данных уравнений извлечем значения X2 и P2. В итоге изменение Pt определяется разностным уравнением 1-го порядка:
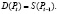
Решение можно пояснить с помощью диаграммы, которая проиллюстрирована на рисунке, где D и S-кривые предложения и спроса, а положение равновесия совпадает с точкой их пересечения Q. В динамической модели D имеет то же значение, что и в статистической, но в данном случае ордината кривой S характеризует величину предложения в конкретный промежуток времени. Цена в первоначальный момент времени будет равна P0. Точка Q0 на кривой D с той же самой ординатой, что и Q0. Во 2-й промежуток времени движение осуществляется по вертикали к точке S на кривой от точки Q1, дающей X2, далее по горизонтали – на кривой D к точке Q2. Дальнейшее продолжение данного процесса формирует график паутины, рассмотренный на рисунке.
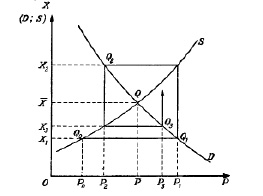
График паутины
Объемы и цены в последующие промежутки времени выступают координатами точек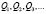 
на кривой спроса D. В данном случае последовательность ряда точек стремится к Q. Точки последовательно размещаются на левой и правой стороне от Q
Итак, характеристики цены Pt стремятся к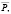 
располагаясь последовательно по обе стороны от 
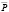. Точно так же дело обстоит и объемами продаж и покупок. Допустим, что D стремится вниз, а S – вверх. Соответственно, движение с затухающими колебаниями появляется в том случае, если кривая D в точке равновесия Q опускается к оси абсцисс OP. Когда углы наклона D и S равны, образуются регулярные колебания. Для случая линейных функций предложения и спроса, можно получить следующее алгебраическое решение:
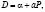
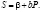
Значения равновесия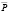 
и 
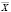будут определяться уравнениями
,
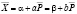то есть
, 
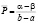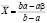. (1)
Дискретная динамическая модель определяется уравнением
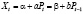. (2)
Для начала найдем решение, дающее равновесие. Для этого положим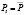 
и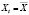 
для всех значений t:
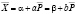. (3)
Извлекаем те же значения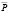 
и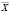 
, что и в (1). Если в каком-либо периоде имелись цены и объемы, создающие условия равновесия, то в динамической модели (2) они сохранятся и будущих периодах. Статистическое равновесие соответствует этой модели. Вычтем уравнение (3) на (2) и положим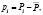 
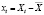. Тогда
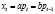. (4)
Уравнения (4) подобны (2), помимо того, что они характеризуют отклонения от уровней равновесия. Эти уравнения являются разностными уравнениями 1-го порядка. Положим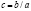 
и подставим его в уравнение (4), так что разностное уравнение относительно Pt будет
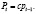
При данном значении P0 в момент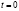 
решение легко получается путем итерации:
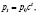
или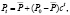 
Объемы продаж и покупок в каждый период можно определить из уравнения (4). Чаще всего кривая спроса идет вниз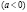 
, а кривая предложения напротив идет вверх 
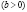, то есть 
В данном случае положим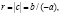 
так что r будет положительно. Тогда
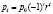
и последовательные значения pt при t=0,1,2,3,…, будут соответственно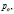 
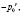
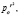
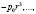так что pt принимает поочередно положительные и отрицательные значения. Таким образом, чередуются и знаки Pt которые поочередно будут располагаться выше и ниже 
.
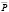Существуют 3 возможности:
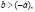угол наклона S (к OP) больше, ежели угол наклона D.
В данном случае r>1 и ряд последовательных значений pt является бесконечно возрастающим по абсолютной величине. Соответственно,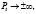 
и имеет место взрывное колебание.
2) 
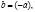углы наклона D и S равны. В рассматриваемом случае r=1, и ряд значений Pt будет состоять из чередования p0 и (–p0) Поэтому Pt будет последовательно больше и меньше P на одну и ту же величину, которая будет равна начальному расхождению 
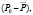то есть в данном случае имеет место регулярное колебание.
3) 
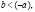угол наклона D (к OP) больше, нежели S. В данном случае r<1, и поочередные Pt уменьшаются по абсолютной величине. Следовательно, 
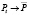последовательно справа и слева, то есть стремится к уровню равновесия с затухающими колебаниями.
В случае (3), чем больше будет – a по отношению к b, то есть чем более круче D по сравнению с S, тем быстрее будут затухать колебания и тем быстрее Pt будет стремиться к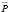 
. Первоначальные возмущения также оказывают наибольшее влияние на амплитуду колебания. Чем дальше P0 от 
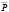, тем больше будет размах колебаний и тем длительнее период времени, необходимый для их прекращения. Следует заметить, что случай (2) с длительными и наиболее правильными колебаниями очень редок, поэтому его можно понимать почти как тривиальным – на его базе не допускается построение никакой теории цикла. Наиболее интересным является случай (3), несмотря на возможное возражение, состоящее в том, что затухающие колебания «невозможны». Но есть наиболее простое развитие модели (3) с затухающими колебаниями, позволяющее представить движение Pt с длительными колебаниями во времени. Для этого вместо кривых предложения и спроса, которые неизменны во времени, возьмем кривые, изменяющиеся под воздействием внешних сил во времени циклично или регулярно, либо случайно и т.д. В таком случае еще до прекращения колебаний, описанных на рисунке, какой-либо сдвиг в кривой D или S приведет к возмущению, в этом случае колебания появятся снова. Например, Q0 могла быть в точке равновесия или вблизи нее до сдвига вверх кривой D к положению, который показан на рисунке. Тогда колебания будут появляться представленным ранее образом, продолжаясь, предположим, до точки Q3, в которых колебательное движение будет нарушено сдвигом вверх кривой S. В итоге, возникает колебательное движение с еще большей амплитудой, постепенно прекращающийся до возникновения какого-нибудь нового возмущения. Для линейной модели допустимо алгебраическое истолкование в случае параллельного перемещения кривых спроса и предложения. Уравнение (2) в таком случае будет иметь вид:
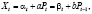
где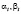 
включают сдвиги в момент t=0,1,2,3,… Разностным уравнением относительно цены будет
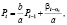(5)
Для того чтобы решить уравнения (5), нужно определить разность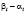 
сдвигов во времени предложения и спроса. Рассмотренная паутинообразная модель чаще всего дает решение, в условиях которой цены в последующие промежутки времени попеременно принимают значения, располагающиеся ниже или выше точки равновесия. Это колебание завершается на протяжении 2-х интервалов, иными словами при наличии двойного запаздывания на стороне предложения. Скорость приспособления к изменившейся обстановке убывает пропорционально увеличению продолжительности запаздывания.
Таким образом, одним из подходов, который объясняет механизм образования рыночного равновесия, можно считать паутинообразную модель, относящаяся к числу динамических (учитывающих фактор времени). Паутинообразная модель описывает процесс формирования равновесия в условиях, когда воздействие участников сделок на изменяющиеся условия рынка растянута по времени.