При передаче энергии от источника в нагрузку обычно используются проводники цилиндрической формы или плоские интегральные схемы, сопротивление которых из-за пренебрежимо малого значения не учитывается [1-3]. Переход к схемам микро, а тем более нанодипазона конструктивно потребовал использования проводников переменного сечения [4], концы которых соответствуют этим диапазонам размеров (10–3 – 10–6 м). Поэтому анализ методов оптимального подключения к микросхемам проводников обычных размеров представляет актуальную задачу. Рассмотрим здесь сопротивление некоторых типов проводников переменного сечения.
Сопротивление резисторов и проводников цилиндрической формы рассчитывается по формуле
,
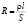где r – удельное сопротивление материала, из которого сделан проводник; S – площадь поперечного сечения проводника; l – длина проводника. Для описания зависимости сопротивления проводника переменного сечения от его размеров необходимо использовать более общее выражение [1,3]:
.
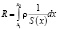Таким образом можно рассчитать сопротивление для проводников самых разных форм. Для большого числа конфигураций можно получить аналитические выражения для расчета сопротивления. В общем случае можно воспользоваться численными методами. Рассмотрим простейшие конфигурации, для которых можно получить аналитическое решение.
Конусовидный проводник (рис. 1а).
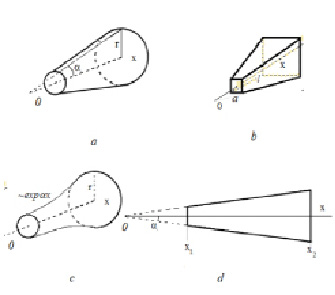
Рис. 1. Проводники переменного сечения с различной зависимостью образующей боковой поверхности: a, b, c –конфигурации сечения; d – сечение проводника a
Если учесть, что площадь поперечного сечения конуса – это площадь окружности с радиусом r, который можно выразить как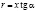 
, то формула для расчета сопротивления проводника будет выглядеть следующим образом:
.
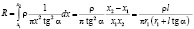Здесь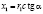 
, 
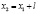. При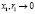 
(игла) сопротивление конусообразного проводника 
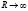. Таким образом, изготовление иглообразных электрических контактов приводит к существенному росту сопротивления проводников. Например, медный цилиндрический проводник с радиусом сечения 1 мм и длиной 1 см будет иметь сопротивление 57,3 мкОм. Такой же проводник переменного сечения, с радиусом, меняющимся от 1 мм до 1 мкм (характерным для элементов микроэлектроники) будет уже иметь сопротивление 57,3 Ом! Это существенно повлияет на режим работы электронных схем.
2) Аналогичными свойствами обладает пирамидоподобная форма проводника (рис.1b). Для четырехгранной усеченной пирамиды со стороной малого основания a и углом между осью и боковой гранью a
.
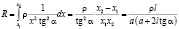Экспоненциально-колбообразный проводник (рис.1c) с образующей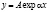 
характеризуется сопротивлением:
.
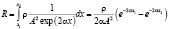При степенной функции образующей колбообразного проводника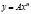 
сопротивление определяется соотношением:
.
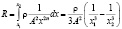На рис. 2 показана нормированная на удельное сопротивление зависимость сопротивления проводника единичной длины от радиуса переменного сечения проводника. Анализ показывает, что неоднородность сечения начинает существенно сказываться на сопротивлении проводника при радиусе меньшем 0.1 мм и возрастает при уменьшении радиуса до 0.01 мм на порядок.
Полученные результаты показывают существенную зависимость сопротивления проводников от формы, проявляющуюся наиболее существенно в области малых сечений. Таким образом, при малых размерах поперечного сечения необходимо учитывать форму проводника.
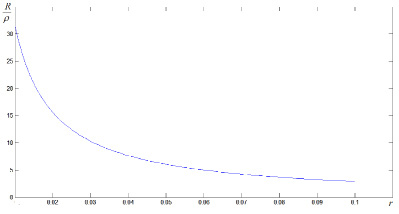
Рис. 2. Изменение сопротивления проводника в зависимости от диаметра провода при малой толщине (l=1)