Существование многочисленных гипотез о физических параметрах, размерах и геометрической форме Земли свидетельствуют, что развитие науки на нашей планете происходило поэтапно. Представление о гравитационном поле Земли постоянно менялось, в XII в. до н.э. Аристотель выдвинул гипотезу о существовании силы притяжения между Землей и другими телами.
Ускорение свободного падения – g – ускорение, придаваемое телу в вакууме силой тяжести, то есть геометрической суммой гравитационного притяжения планеты (или другого астрономического тела) и сил инерции, вызванных её вращением. В соответствии со вторым законом Ньютона, ускорение свободного падения равно силе тяжести, воздействующей на объект единичной массы [1]. Экспериментально установлено, что ускорение свободного падения не зависит от массы падающего тела, но зависит от географической широты местности и высоты h подъема над земной поверхностью, что обеспечивается эллипсоидальной формой земной поверхности и ее вращением вокруг своей оси [2].
В настоящее время существует множество экспериментальных способов определения ускорения свободного падения, все они делятся на две категории: статистические и динамические методы. В статических методах тело, участвующее в измерениях, находится в момент измерения (фиксации отсчета) в покое, измеряются смещение тела или давление, вызванное весом тела. Приборы, служащие для измерения силы тяжести статическим методом, называются гравиметрами [3].
Широкое распространение получили маятниковые способы, относящиеся к динамическим методам, в которых наблюдают движение тела в гравитационном поле. Последнее представляет собой силовое поле, обусловленное притяжением масс Земли и центробежной силой, которая возникает вследствие суточного вращения планеты. Гравитационное поле характеризуется силой тяжести, потенциалом силы тяжести и различными его производными.
Маятниковые измерения – относительный метод, позволяющий определить ускорение силы тяжести между гравиметрическими пунктами. Гравиметрическими пунктами называются точки на земной поверхности, в которых измерено ускорение силы тяжести и определены плановые координаты и высоты. Сущность способа заключается в наблюдении свободных колебаний одного и того же маятника на разных пунктах. Преимуществами таких измерений являются: независимость результатов измерений, точность, независимость от продолжительности гравиметрического рейса и от сложности поля [3]. В данной статье проанализированы два способа определения ускорения свободного падения: с помощью физического и оборотного маятников.
Физический маятник – это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точку О, не совпадающую с центром масс С (рисунок).
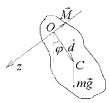
Физический маятник
Использование произвольных физических маятников удобно для нахождения отношений значений g в различных точках поля тяготения, но при определении самого значения g возникает трудность точного определения момента инерции маятника, что исключается в методе оборотного маятника, т.к. в его расчетных формулах отсутствует величина момента инерции маятника J0 [5].
Метод оборотного маятника основан на известном свойстве двух точек физического (точки подвеса и точки качания), при последовательном подвешивании маятника в которых его период остается неизменным. Расстояние между этими точками определяется приведенной длиной физического маятника lпр.
Таким образом, если у физического маятника найдены две сопряженные точки, когда периоды колебаний на них T1 и T2 совпадают с точностью до 2-3 с (для этого необходимо выбрать такие точки на маятнике, для которых время одинакового числа колебаний будет отличаться не более чем на 0,3 с), тогда для определения g достаточно точно измерить T0 =T1 = T2 и lпр равное расстоянию между этими точками [4].
Т.к. экспериментально достаточно сложно выбрать точки так, чтобы T1 = T2, то для повышения точности можно использовать теорему Штейнера, на основании которой конечная формула определения ускорения свободного падения будет выглядеть так:
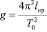 ,
,
где lпр – расстояние между выбранными точками на маятнике, а
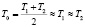 .
.
В ходе эксперимента при N=50, где N – количество колебаний и lпр = 0,230 м было проведено несколько серий измерений, по результатам которых составлена таблица.
|
№ п/п |
t(rc1), с |
t(rc2),с |
T(rc1), с |
T(rc2), с |
g, (м/с2) |
|
1 |
47,8 |
47,9 |
0,956 |
0,958 |
9,904288 |
|
2 |
48,1 |
48,3 |
0,962 |
0,962 |
9,801600 |
|
Ср. |
47,95 |
48,10 |
0,959 |
0,962 |
9,852944 |
По данным таблицы получено среднее значение ускорения свободного падения gср= 9,852944 м/с2= =985244 мГал. По формуле
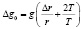
была рассчитана относительная погрешность полученной величины ?gср= ±0,1125367 м/с2=1125367 мГал. Таким образом, было установлено, что значение gтеор= 9,80665 м/с2=980665 мГал (ускорение свободного падения на уровне моря и широте 45°), которое принято за фундаментальное, входит в доверительный интервал экспериментально полученного значения ускорения свободного падения
9.7404073 м/с2 ≤gср≤ 9.9654807 м/с2 [5].

