Системы прогнозирования и управления продажами довольно обширны и в основном имеют широкий профиль применения при организации работы производства или точки сбыта. Однако функциональность таких систем непременно приводит к её усложнению и необходимости дополнительного конфигурирования под узкоспециализированные задачи. Всё это, в конечном счете, позволяет сделать вывод о целесообразности оценки эффективности работы автоматизированной сбора заказов и планирования продаж в производстве хлебопекарной продукции. В этой связи актуальной задачей является исследование методов принятия управленческих решений и оценка их эффективности при изменении уровня конкуренции.
Анализ стратегий управления [1,2], лежащих в основе работы автоматизированных систем принятия решений показывает, что в подавляющем большинстве случаев системы управления продажами используют статические модели планирования, основанные на статистическом анализе потоков заказов.
Пусть интенсивность потока заказов определяется функцией P(t). Тогда количество заказов, появившихся за время ?t = t2 – t1 и претендующих на обслуживание, можно определить как:
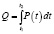 . (1)
. (1)
Если основываться на доминировании интересов производства и допустить, что мощность С (Capacity) всех производственных единиц одинакова, то нахождение интервала поступления заказов h (headway) может быть сведено к решению следующего уравнения:
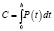 . (2)
. (2)
В случае равномерного распределения потока заказов P(t) = l получаем:
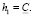 (3)
(3)
Выражения (2) и (3) предполагают полную загрузку производственных единиц. На практике при расчете интервала поступления заказов учитывают и показатели рентабельности. Существенное влияние на нее оказывает уровень заполняемости производства L (Loading), при котором сохраняется его рентабельность. Тогда эффективная загрузка производственной единицы D может быть найдена как:
D = СL, (4)
где 0 < L ≤ 1.
Тогда (2) и (3) будут выглядеть как:
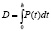 ; (5)
; (5)
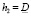 . (6)
. (6)
С учетом (4) h1 > h2.
Если ориентироваться на потребителей поставок и опираться на задание среднего времени ожидания, которое заказы проводят в очереди T (Time Waiting), то для постоянного потока заказов с P(t) =l интервал поступления заказов может быть найден как:
h = 2Тw, (7)
поскольку время ожидания
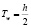 .
.
Тогда из (3) можно определить С:
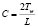 . (8)
. (8)
Интересы акторов процесса продаж противоречивы. Производство заинтересовано в максимальном заполнении мощностей производства (3), а заказы в минимальном времени ожидания – (8). Противоречивость интересов участников переводит процесс управления продажами в разряд задач многокритериальной оптимизации. В какой-то мере коэффициент L позволяет балансировать интересы.
Потоки заказов подчиняются многочисленным ритмам – суточным, недельным, сезонным. Они зависят и от графика проведения массовых мероприятий (праздников). Это учитывается при составлении расписания составления заказов – интервалы в течение суток изменяются. В управлении доминирует тенденция к жесткому их соблюдению до очередного переопределения.
Соотношения (1) – (8) справедливы при расчете параметров систем принятия решений без учета конкуренции. В реальном мире за заказы идет конкурентная борьба между несколькими производственными компаниями, предлагающими различные условия поставок. Статическое планирование не может обеспечить реакцию на динамические изменения характеристик потоков заявок и состояния технологической оснастки производств.
Низкая эффективность работы программно-аппаратных комплексов управления продажами в пищевом и, в частности, хлебопекарном производстве может быть связана с тем, что они не учитывают конкуренцию на рынке. Для решения этой проблемы необходимо ввести новые оценки качества алгоритмов управления, в частности, их способность оптимизировать работу объекта управления при воздействии на него конкурирующих субъектов. Этой цели можно достичь при создании моделей управления продажами и исследовании их функциональности в широком диапазоне параметров.

