Рассмотрим поперечное сечение проводника в системе координат XOY (рисунок 1). Ширина проводника b, его толщина 
, длина проводника 
, . По проводнику протекает постоянный ток J с соответствующей плотностью
. Разобьем поперечное сечение проводника на бесконечно большое число нитей тока сечением 
. Положение элементарной площадки 
характеризуется текущими координатами 
. Напряженность магнитного поля, создаваемая элементарной нитью тока в заданной точке 
определится выражениями
(1)
(2)
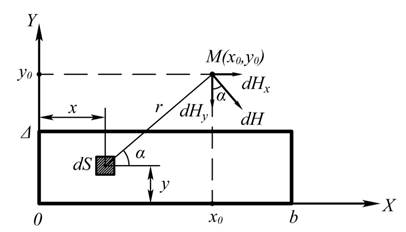
Рисунок 1 Поперечное сечение прямоугольного проводника с током
Указанные выражения получены из формул и соотношений, следующих из рисунка 1
Так как в моментном двигателе [4] основным является поток, направленный перпендикулярно ширине пластины b, направленной по оси X, то внимание в дальнейшем будем обращать на компоненту напряженности 
. В данной работе предполагаем, что плотность тока 
по всему сечению проводника одинакова 
. Нормальная к поверхности проводника компонента напряженности определяется двойным интегралом от выражения (2)
(3)
Так как в дальнейших исследованиях предполагается учитывать, что плотность тока является функцией 
, первое интегрирование проводим по y в пределах от 0 до . Учитывая, что интеграл является табличным [5], получаем
(4)
Дальнейшее определение интеграла (4) проведено в программе MathCad. Для этого выражение (4) преобразовано к виду
(5)
В выражении (5) произведены следующие замены: 
; 
; 
; 
.
В результате вычислений интеграла (5) в программе MathCad получено выражение
,
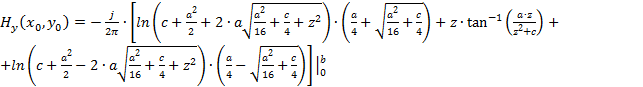которое после замены переменных можно представить в виде
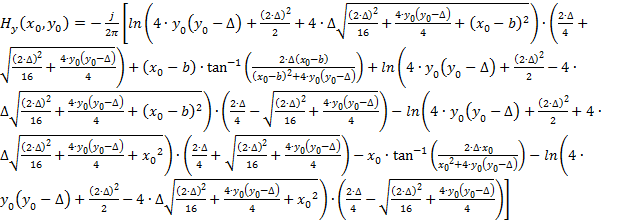. (6)
После подстановки в полученное выражение значений 
учитывая ток, протекающий по проводнику 
и связь между напряженностью и индукцией в немагнитном пространстве 
, получена графическая зависимость (рисунок 2), связывающая нормальную к поверхности проводника индукцию магнитного поля на удалении от упомянутой поверхности на 0.1 мм и координату, направленную вдоль ширины проводника.
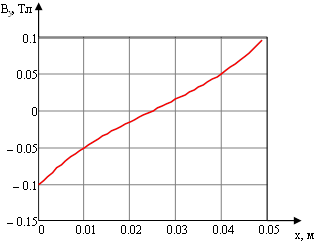
Рисунок 2 Аналитически полученная зависимость индукции магнитного потока
вдоль ширины проводника
Аналогичные исследования были проведены с помощью программного продукта конечноэлементного моделирования COMSOL Multiphysics. Решение численными методами вышеупомянутой задачи при тех же самых исходных данных приведено на рисунке 3. При этом распределение индукции магнитного потока, направленной нормально к поверхности пластины вдоль ширины пластины показано на рисунке 4.
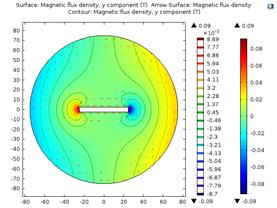
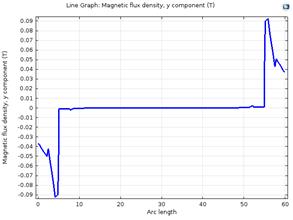
Рисунок 3 Решение задачи в среде Рисунок 4 Индукция магнитного
COMSOL Multiphysics поля вдоль ширины пластины, полученная
в COMSOL Multiphysics
Сравнивая результаты, отображенные на рисунках 2 и 4, можно отметить следующее:
- общая закономерность изменения индукции вдоль ширины проводника заключается в том, что максимумы индукции наблюдаются у боковых краев проводника, а минимальные значения индукции (смена знака) - в центре поверхности проводника;
- рассчитанные значения индукции (максимумы порядка 0.1 Тл) показывают, что в ряде случаев, когда индукция основного потока в зазоре (при отсутствии номинального тока в проводнике) находится в пределах 0.5 - 1.0 Тл, влияние магнитного потока, вызванного током в проводнике может изменить ожидаемые расчетные эксплуатационные характеристики двигателя.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 14-08-31068 мол_а