На сегодняшний день одним из важнейших навыков для любого специалиста является умение решать дифференциальные уравнения. Необходимость в решении дифференциальных уравнений возникает во многих прикладных задачах. В своей статье мы рассмотрим применение теории дифференциальных уравнений в непрерывных моделях экономики. Такие модели достаточно эффективны при исследовании эволюции экономических систем на длительных интервалах времени; они являются предметом исследования экономической динамики.
При решении дифференциальных уравнений первого порядка можно пользоваться моделями: модель естественного роста выпуска; динамическая модель Кейнса; неоклассическая модель роста.
Рассмотрим более подробно динамическую модель Кейнса.
Пусть Y(t), E(t), S(t), I(t) – соответственно национальный доход, государственные расходы, потребление инвестиции. Все эти величины рассматриваются как функции времени t. Тогда справедливы следующие соотношения:
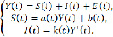 (1)
(1)
где a(t) – коэффициент склонности к потреблению; b(t) – автономное потребление; k(t) – норма акселерации.
Сумма всех расходов должна быть равной национальному доходу – этот баланс отражен в первом уравнении системы (1). Общее потребление состоит из внутреннего потребления некоторой части национального дохода в народном хозяйстве плюс конечное потребление – эти составляющие показаны во втором уравнении системы (1). Размер инвестиций не может быть произвольным: он определяется произведением нормы акселерации, величина которой характеризуется уровнем технологии и инфраструктуры данного государства, на предельный национальный доход.
Требуется найти динамику национального дохода или Y как функцию времени t.
Подставим выражения для S(t) из второго уравнения и I(t) из третьего уравнения в первое уравнение. После приведения подобных, получаем линейное неоднородное дифференциальное уравнение первого порядка для функции Y(t):
Y’ = 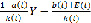 . (2)
. (2)
Примем основные параметры задачи a, b, k за постоянные числа. Тогда уравнение (2) упрощается до случая линейного дифференциального уравнения первого порядка с постоянными коэффициентами:
Y’ = 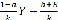 . (3)
. (3)
В качестве частного решения уравнения (3) возьмём равновесное решение,
когда Yꞌ=0, т.е. 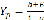 .
.
Общее решение однородного уравнения дается формулой
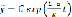 ,
,
так что общее решение уравнения (3) имеет вид:
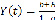 + C
+ C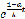 .
.

