Многие задаются вопросом: что такое статистическая гипотеза и зачем её нужно проверять? Статистическая гипотеза – это любое предположение о генеральной совокупности, проверяемое по выборке. Выдвигается основная (нулевая) гипотеза H0 и проверяется, не противоречит ли она имеющимся эмпирическим данным. Конкурирующей (альтернативной) называют гипотезу H1, которая противоречит нулевой, и которую принимают, если отвергнута основная гипотеза. В результате статистической проверки гипотезы могут быть допущены ошибки двух родов. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза; вероятность совершить такую ошибку обозначают α и называют её уровнем значимости. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза, вероятность которой обозначают β, а мощностью критерия является вероятность 1 – β.
Проверка статистических гипотез тесно связана с теорией оценивания параметров. В экономике для выяснения того или иного случайного факта часто гипотезам, которые можно проверить статистически, т. е. опираясь на результаты наблюдений в случайной выборке. Рассмотрим на примере.
Нужно проверить нулевую гипотезу о том, что значение a0 = 40 является математическим ожиданием нормально распределенной случайной величины при пятипроцентном уровне значимости α для двусторонней и односторонней критических областей, если в результате обработки выборки объёма n = 10 получено выборочное среднее 
в = 38, а несмещённое среднее квадратичное отклонение s = 3,6.
Т. к.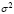 
неизвестно, то статистика критерия вычисляется по формуле
.
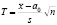1) Для двусторонней критической области имеем:
H0: a = 40, H1: a ≠ 40, tкр = 2,26 (по таблице критических точек распределения Стьюдента tкр = t α; n–1 = t 0,05; 9).
Tнабл =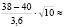
– 1,76.
Т.к. |Tнабл| < tкр , то принимаем основную гипотезу H0.
2) Для левосторонней критической области:
H0: a = 40, H1: a < 40, tкр = 1,83.
Т.к. Tнабл > – tкр , то принимаем основную гипотезу гипотезу H0.
3) Для правосторонней критической области:
H0: a = 40, H1: a > 40, tкр = 1,83.
Т.к. Tнабл < tкр , то принимаем основную гипотезу гипотезу H0.
Можно сказать, что проверка статистических гипотез – необходимая методика, используемая для получения данных в математической статистике. Задача проверки статистических гипотез возникает в разных сферах человеческой деятельности, в том числе и в экономике. Она позволяет с единой точки зрения трактовать выдвигаемые практикой различные задачи математической статистики (оценка различия между средними значениями, проверка гипотезы постоянства дисперсии, проверка гипотезы независимости, проверка гипотез о распределениях и т. п.).