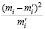При обследовании 2000 тепличных хозяйств было отобрано 110 теплиц. Распределение их по объёму совокупных ежегодных продаж (ден. ед.) приведено в таблице:
|
Объём совокупных ежегодных продаж, ден. ед. |
менее 500 |
500-1000 |
1000-1500 |
|
Число теплиц |
8 |
20 |
52 |
|
Объём совокупных ежегодных продаж, ден. ед. |
1500-2000 |
2000-2500 |
Всего |
|
Число теплиц |
18 |
12 |
110 |
Используя критерий χ2 Пирсона, при уровне значимости α = 0,05 проверить гипотезу о нормальном распределении случайной величины Х – объёма совокупных ежегодных продаж.
По условию 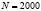 ,
, 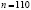 . Найдём середины интервалов.
. Найдём середины интервалов.
|
|
250 |
750 |
1250 |
1750 |
2250 |
Всего |
|
|
8 |
25 |
47 |
18 |
12 |
110 |
Найдём числовые характеристики выборки:
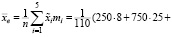
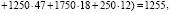
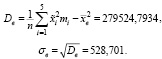
Исправленное выборочное среднее квадратическое отклонение:
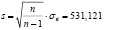
Используя критерий согласия Пирсона, при уровне значимости α = 0,05 проверим гипотезу 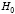 : о нормальном распределении случайной величины Х с параметрами а = х̄в = 1255 и
: о нормальном распределении случайной величины Х с параметрами а = х̄в = 1255 и 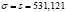 при альтернативной гипотезе
при альтернативной гипотезе 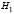 : случайная величина Х не распределена по нормальному закону.
: случайная величина Х не распределена по нормальному закону.
Вычислим вероятности 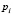 попадания случайной величины
попадания случайной величины 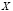 в заданные интервалы с помощью функции Лапласа по формуле:
в заданные интервалы с помощью функции Лапласа по формуле:
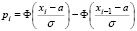 .
.
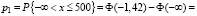
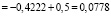 ;
;
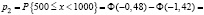
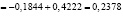 ;
;
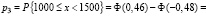
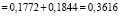 ;
;
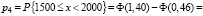
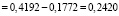 ;
;
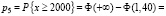
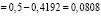 .
.
Для проведения расчётов заполним вспомогательную таблицу:
|
|
интервал
|
частота
|
теоретическая частота
|
|
|
1 |
менее 500 |
8 |
7,78 |
0,0364 |
|
2 |
500-1000 |
25 |
23,78 |
0,0513 |
|
3 |
1000-1500 |
47 |
36,16 |
1,3120 |
|
4 |
1500-2000 |
18 |
24,20 |
2,7913 |
|
5 |
2000-2500 |
12 |
8,08 |
1,0896 |
|
Σ |
– |
110 |
110 |
5,2806 |
Наблюдаемое значение критерия согласия Пирсона
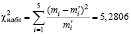 .
.
По таблице приложения 3 по заданному уровню значимости α = 0,05 и числу степеней свободы l = 5 – 3 = 2 найдём критическое значение
χ2кр(α;l ) = χ2кр(0,05;2) = 5,99.
Т. к. χ2набл < χ2кр, то нулевая гипотеза о нормальном распределении принимается как не противоречащая опытным данным.


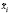
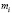
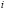
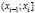
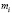
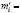 npi
npi