При обследовании 2000 тепличных хозяйств было отобрано 110 теплиц. Распределение их по объёму совокупных ежегодных продаж (ден. ед.) приведено в таблице:
|
Объём совокупных ежегодных продаж, ден. ед. |
менее 500 |
500-1000 |
1000-1500 |
|
Число теплиц |
8 |
20 |
52 |
|
Объём совокупных ежегодных продаж, ден. ед. |
1500-2000 |
2000-2500 |
Всего |
|
Число теплиц |
18 |
12 |
110 |
Найти:
а) вероятность того, что средний объём продаж во всех тепличных хозяйствах отличается от среднего объёма продаж в выборке не более чем на 100 ден. ед. (по абсолютной величине);
б) границы, в которых с вероятностью 0,97 заключена доля теплиц, объём продаж которых не более 1000 ден. ед.;
в) каким должен быть объём выборки, чтобы те же границы для доли теплиц, объём продаж которых не более 1000 ден. ед., можно было гарантировать с вероятностью 0,999?
Решение. Предварительно находим числовые характеристики выборки:
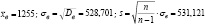
а) Для вычисления искомой вероятности применим формулу
,
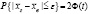где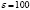 
, 
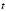– аргумент функции Лапласа, который в случае неизвестного σг и известного объёма генеральной совокупности 
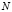, определяется по формуле:
Имеем
.
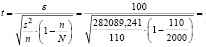
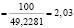Тогда
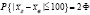(2,03) = 2 ∙ 0,4788 = 0,9576.
б) По данной таблице найдём долю теплиц с объёмом продаж не более 1000 ден. ед.:
.
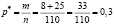Пусть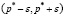 
– интервал, в который с вероятностью 0,97 попадает доля 
.
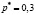Значение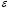 
определяется по формуле:
.
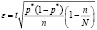Т. к. γ = 0,97 =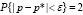 
Ф(t), то
Ф(t) = 0,97 / 2 = 0.485.
По таблице находим t = 2,17.
Тогда
.
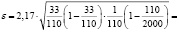
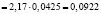Окончательно находим доверительные границы:
;
.
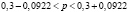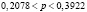в) Объём выборки определяем по формуле:
,
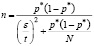где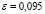 
(см. п. б), т. к. по условию задачи границы те же).
Для доверительной вероятности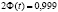 
находим по таблице значение аргумента 
.
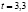Имеем
.
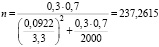Окончательно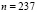 
.