Теория вероятности представляет собой раздел математики, изучающий закономерности случайных явлений, событий и значений. В современном мире, для получения наиболее достоверных количественных значений экономических показателей, все более актуально применение математического аппарата теории вероятности, устанавливающего взаимосвязь между различными случайными параметрами, что помогает принимать обоснованные решения в управлении экономическими процессами. Задачи, решаемые данным способом, имеют огромную практическую значимость, позволяя упростить довольно громоздкие вычисления.
Исходным понятием при построении вероятностных моделей, в задачах по принятию решений, является опыт. Первым шагом становится выделение элементарных событий, при которых возможно два исхода: событие произошло, либо не произошло. Совокупностью всех возможных исходов в проводимом опыте, называется пространство элементарных событий, состоящих из конечного числа элементов.
Применение вероятностного метода подразумевает прохождение нескольких этапов в процессе решения. Во-первых, необходимым условием является переход от экономических, управленческих и технологических показателей. На полученной числовой базе формируются вероятностные модели системы управления, процедуры принятия решений. Во-вторых, проведение расчетов и как следствие получение числовых математических выводов. В-третьих, интерпретация математического анализа относительно к реальной ситуации и принятие соответствующего решения.
Рассмотрим данный алгоритм применимо к решению задач по выработки стратегии работы страховых компаний. Наступление, либо не наступление страхового случая есть величина случайная. В связи с этим страховые компании анализируют статистические данные по поводу наступления страховых случаев, с учетом условий при которых они наступили. Для установления ставки страхового взноса, в условиях безубыточности компании, оценивается вероятность наступления страхового случая.
Пусть страховая компания заключает договоры страхования сроком на 1 год, на Т рублей каждый. Страховой случай происходит с вероятностью p и не происходит с вероятностью q=1-p. Таким образом, закон распределения случайной величины Xi – количества страховых случаев у одного, i-го, страхователя. Число людей, застрахованных в компании, составляет 1300 клиентов.
Математическое ожидание дискретной случайной величины Xi называется сумма произведений ее возможных значений на соответствующие им вероятности:
M(X) = x1p1+x2p2+...+xnpn
или M(X)= ∑ni =1xipi (1)
Дисперсией случайной величины называется математическое ожидание квадрата отклонения этой величины от ее математического ожидания и равно:
D(X) = M(X2) – M2(X) ,
где M(X2) = ∑ni =1xi2pi (2)
Случайная величина X = ∑ni =1Xi ; количество страховых случаев у страхователей имеет математическое ожидание M(X)=np и дисперсию D(X)=npq, как следствие среднее квадратичное отклонение
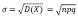 .
.
Случайная величина X распределена по нормальному закону в силу централизованной предельной теоремы. В среднем страховая компания должна будет выплатить npT страховых возмещений, с каждого страхователя по pT рублей страхового взноса. Исходя из этого, в среднем баланс страховой компании будет нулевым. Величина страховых возмещений – случайна, и может оказаться больше и привести к убыткам компании, либо меньше, образуя прибыль. Для безубыточности страховой компании, сумма взноса должна быть больше рассчитанной, величину которого можно определить с помощью интервальных оценок.
Реальную ставку обозначим через p ̃> p, в этом случае страховая компания соберет с-го количества страхователей сумму равную np ̃T рублей. Обозначим через f(x) = y, вероятность того, что компания не понесет убытков. При этом вероятность, что количество страховых случаев не более np ̃, есть P(x < xp ̃) = y.
Нормальное распределение или распределение Гаусса, есть распределение вероятностей, которое в одномерном случае задается функцией плотности вероятности, совпадающей с функцией Гаусса:
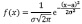 , (3)
, (3)
где a=M(X)(1), 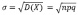 (2).
(2).
Используя нормальный закон распределения для случайной величины X, имеем:
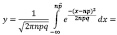
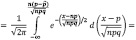
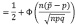 ;
;
В данном случае через Ф обозначена интегральная функция Лапласа:
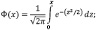 (4)
(4)
Теорема. Если в серии nнезависимых испытаний вероятность наступления события в каждом отдельном испытании постоянна и 0 < p < 1 , то вероятность того что событие наступит от a до b раз равняется формуле (4).
Зададим вероятность y = 0,87 , что страховая компания не разорится, соответственно вероятность наступления страхового случая равна p = 0,13. Число клиентов, застрахованных в компании, равно n = 1300 .
Формула Лапласа (4) на практике используется в случае, если npq ≥ 10. Если же npq < 10, то формула приводит к довольно большим погрешностям.
Пользуясь таблицей значений функции Лапласа:
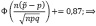
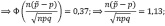
Исходя из этого, найдем ставку страхового процента (p ̃):
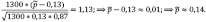
Вследствие полученных результатов, можно сделать вывод о том, что чем больше риск для страховой компании, тем больше величина страхового взноса. Данная закономерность обусловлена ожиданиями предстоящих расходов компании. В среднем, расходы по наступлению страховых случаев, какого либо типа, должны быть меньше, чем доходы в виде страховых взносов от страхователей.
Применение экономико-математических методов позволяет провести качественный и количественный анализ экономических явлений, способствует количественной оценки значений риска и рыночной неопределенности, что позволяет выбрать наиболее оптимальное решение. Математические модели в первую очередь позволяют абстрактно представлять различные хозяйственные ситуации с дальнейшей оценкой последствий при выборе решений, что существенно упрощает поставленную задачу.

