В наше время общество не может себе представить жизнь без применения математики в экономике. Одним из самых распространенных расчетов в банковской деятельности является расчет кредитных ставок.
Итак, рассмотрим некоторые элементы финансовой математики:
Существует такое понятие как эффективная процентная ставка.
Смысл эффективной процентной ставки заключается в том, что она призвана отражать реальную стоимость кредита с точки зрения заёмщика, то есть учитывать все его побочные выплаты, непосредственно связанные с кредитом (помимо платежей по самому кредиту).
Следующий элемент это – непрерывное начисление сложных процентов.
Как известно, для стремящегося к бесконечности числа x существует предел
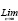
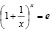
где e = 2,718281828... – основание натуральных логарифмов. Эта формула называется вторым замечательным пределом. Из неё следует, в частности, что справедливо соотношение
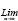
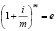
Значит, если капитализация процентов осуществляется достаточно часто, например, ежедневно, то эффективную процентную ставку можно приближённо найти следующим образом: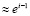 
И, наконец, интенсивность процентов.
Интенсивность процентов δ – это мгновенная относительная скорость накопления средств
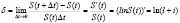
Т.к.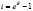 
, то коэффициент накопления за время t можно записать в виде
.
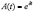Интенсивность процентов удобно использовать для изучения накоплений в случае изменяющихся процентных ставок. В этом случае: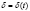 
и
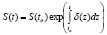
Разберем некоторые способы вычисления процентных ставок:
Для начала возьмем простейший способ вычисления процентных ставок.
Получения кредита размером S0 заемщик обязан совершить платежи Ro, R1, R2, ..., Rn в моменты времени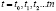 
, соответственно (включая платежи по самому кредиту, страховые выплаты ,побочные комиссии и т.д.), то эффективная процентная ставка i находится из соотношения:
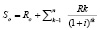
Эффективная процентная ставка служит главным образом для сравнения различных банковских предложений, и при её вычислении точные даты совершения платежей обычно неизвестны. Поэтому, если платежи совершаются через одинаковые промежутки времени продолжительностью τ (ежемесячно, ежеквартально и т.д.), то данная формула примет вид:
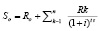
Теперь мы рассмотрим несколько примеров решения задач.
В качестве первого, проанализируем методы простых процентов:
Предположим, что вкладчик положит сумму 100 тыс. руб. в банк, предлагающий 10% годовых. Допустим, банк использует метод простых процентов для начисления процентов по вкладу. Нам необходимо найти сумму, которая будет лежать на счету вкладчика через полгода.
Воспользуемся методом вычисления простых процентов. Формула для вычисления выглядит так: S(t)=(1+it)So, где t – момент времени, So – первоначальный размер вклада (задолженности), S(t) – конечная денежная сумма, a i-процентная ставка.
В нашей задаче дано: = 100000; t = 1/2; 10% = 0,1.
Найти: S(t)=?.
Решение:
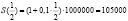
Таким образом, через полгода на счету вкладчика будет сумма, равная 105 тысячам рублей.
Теперь перейдем к методу сложных процентов:
Предположим, что вкладчик положил сумму 100 тыс. рублей все в тот же банк, предлагающий вклады под 10% годовых. Пусть банк использует метод сложных процентов по вкладу. Найти сумму, которая будет лежать на счету вкладчика через полгода.
Воспользуемся методом вычисления сложных процентов. Формула для вычисления выглядит так:
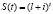So,
где t – момент времени, So – первоначальный размер вклада (задолженности), S(t) – конечная денежная сумма, a i – процентная ставка.
В нашей задаче дано:=100000; t = 1/2; 10% = 0,1;
Найти: S(t)=?.
Решение:
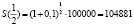
Из решения следует, что через полгода на счету вкладчика будет сумма, равная 104881 рублей.
Далее сравним простой и сложный методы процентов:
Рассмотрим пример, показывающий, к каким расхождениям может привести использование простых процентов для полугодового вклада, когда процентная ставка составляет 300% годовых.
Итак, данные задачи: S – размер вклада; t = 1/2 – время; 300% = 3 – процентная ставка.
Если бы банк использовал простые проценты, то итоговую сумму искали бы по формуле:
S(t) = (1 + it)So.
Подставляя значения, получаем:
.
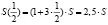А при использовании сложных процентов, вычисления производились бы по формуле:
.
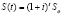В данной задаче получаем:
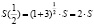
Разница в результатах составляет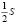 
или 25% относительно сложного итога.
Рассмотрим еще один пример. В банк на 3 года положили 30000 рублей под 10% годовых на депозит. а) Найдите насколько прибыльнее был бы вариант, когда годовой доход добавлять к счету, на который в будут начисляться проценты, чем вариант, когда проценты каждый год забираются клиентом? б) Какая будет разница через 10 лет?
Решение.
а) Для первого случая используем формулу для вычисления сложных процентов:
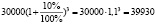
прибыль в этом случае равна 39930 – 30000 = 9930
Во втором случае годовой доход будет равен
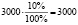
тогда прибыль за три года будет равна 3000 · 3 = 9000.
Первый метод будет выгоднее второго на
9930 – 9000 = 930 рублей
б) Для первого случая используем формулу для вычисления сложных процентов:
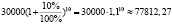
прибыль в этом случае равна: 77812.27 – 30000 = 47812.27
Во втором случае годовой доход будет равен:
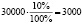
соответственно прибыль за десять лет будет равен: 3000 · 10 = 30000
Первый метод будет выгоднее второго на
47812.27 – 30000 = 17812.27 рублей
На основании данной задачи, можно сделать следующие выводы: а) наиболее прибыльный вариант составил 900 рублей; б) через 10 лет разница составит 17812,27 руб.
Существование экономики без математических методов решения различных задач невозможно. Мы рассмотрели лишь малую долю жизненных примеров взаимосвязи математики и экономики в жизни современного человека. Всем наверняка придется ни один раз столкнуться с кредитованием, и каждый выбирает условия, выгодные ему в данной ситуации. А для того, чтобы сделать правильный выбор, необходимо проверить все, ведь в таких ситуациях мелочей не бывает, а любая ошибка может дорого стоить. Для этого мы рассмотрели несколько распространенных способов расчета процентной ставки и предложили яркие примеры с вычислениями. Мы выяснили разницу между простыми и сложными процентами.