Для кривых второго порядка возникает вопрос, имеющий практическое значение: действительны ли для параболы, эллипса и гиперболы метрические соотношения подобные тем, которые существуют для окружности (свойства касательной и секущей и другие).В данной статье покажем, что такие метрические соотношения существуют.
I. Парабола
Лемма 1. Пусть точка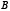 
лежит на хорде 
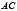параболы 
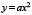или на ее продолжении и, кроме того, прямая 
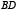параллельна оси 
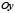, причем точка 
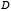лежит на параболе. Тогда
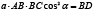, (1)
где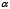 
– угол, составленный хордой с горизонталью.
Доказательство. Решим сначала графическим путем квадратное уравнение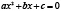 
. Для этого построим на одном чертеже графики функци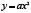и 
и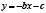 
. Очевидно, абсцисса 
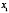и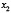 
точек пересечения 
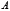и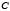 
параболы с прямой будут корнями данного уравнения.Сделав затем некоторые дополнительные построения, найдем из чертежа (рис. 1):
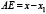и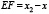 
.
Далее, перемножая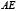 
и 
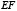, получим (2):
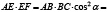
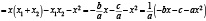
Кроме того, нетрудно заметить, что
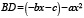(3)
Из равенств (2) и (3) следует (1).Аналогичным доказывается лемма и в том случае, когда точка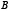 
будет внешней по отношению к параболе (рис. 2).
II. Эллипс
Лемма 2. Пусть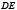
– вертикальная или горизонтальная и 
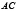– наклонная хорды эллипса 
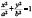и, кроме того, 
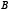– точка пересечения хорд или точка, лежащая на продолжении их. Тогда
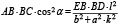, (4)
где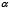 
– угол, составленный наклонной хордой с осью 
,
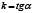и 
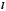равно 
или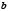 
, в зависимости от того, вертикальной или горизонтальной будет хорда 
.
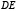Доказательство. Пусть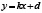 
– уравнение прямой, проходящей через концы наклонной хорды. Решив его совместно с уравнение эллипса, получим квадратное уравнение:
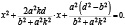
Очевидно, что в данном случае
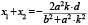и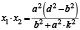 
.
Далее, из чертежа (рис.3) найдем:
,
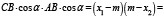
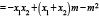или
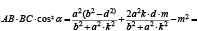
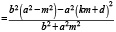(5)
Замечая, что
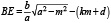и
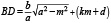
получим:
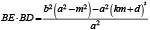(6)
Таким образом, принимая во внимание равенства (5) и (6), будем иметь
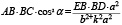(7)
В том случае, когда хорда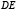 
горизонтальна, а также тогда, когда точка 
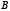будет внешней по отношению к эллипсу (рис.4), теорема доказывается по аналогии.
Частный случай: при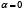 
из формулы (7) следует соотношение:
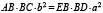. (8)
III. Гипербола
Лемма 3.Пусть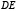 
– вертикальная или горизонтальная и 
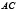– наклонная хорды гиперболы
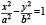
и, кроме того,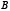 
– точка пересечения хорд или точка, лежащая на продолжении их.
Тогда:
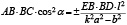, (9)
где, 
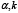и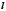 
имеют тот же смысл, что и для эллипса; при этом знак плюс или минус в правой части равенства берется в соответствии с тем, внутренней или внешней будет хорда 
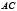по отношению к гиперболе. Доказательство леммы (3) аналогично тому, что мы имели для эллипса. Частный случай: если хорда 
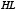параллельна оси 
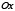и хорда 
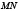параллельна оси 
и, кроме того,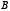 
– точка пересечения одной из них с продолжением другой (рис.5 и 6), то из леммы (3) можно получить соотношение
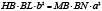(10)
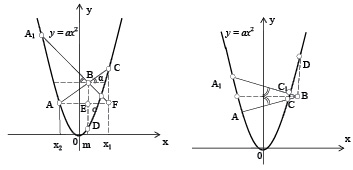
Рис. 1. Рис. 2.
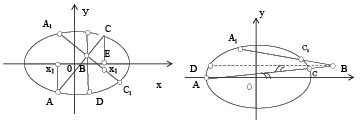
Рис. 3. Рис. 4.
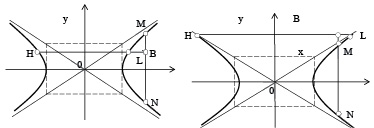
Рис. 5. Рис. 6.
Так как через точку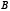 
, не лежащую на кривой, можно провести всякий раз по две прямых (две хорды, или две секущих, или секущую касательную), составляющих с осью 
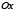одинаковые углы, то из рассмотренных выше лемм, а также их частных случаев, непосредственно вытекают следующие теоремы.
Теорема I. Произведения отрезков хорд кривой второго порядка, проходящих через данную точку и, составляющих с ее осью одинаковые углы, равны между собой.
Теорема II. Произведения секущих кривой второго порядка, проходящих через данную точку и составляющих с ее осью одинаковые углы, на их внешней части, равны между собой.
Теорема III. Если секущие и касательные кривой второго порядка, проведенные из данной точки, составляют одинаковые углы с ее осью, то квадрат касательной будут равен произведению секущей на ее внешнюю часть.
Теорема IV. Если хорда центральной кривой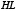 
параллельна оси 
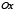и хорда 
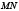параллельна оси 
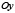и, кроме того, 
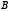– точка пересечения хорд или точка, лежащая на продолжении их, то 
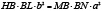. В частности, для окружности и равносторонней гиперболы (b = a) будем иметь: 
.
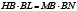Отметим также, что теоремы I, II и III (с учетом того, что касательная если предельное положение секущей) можно объединить в одну теорему: есл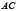и 
и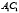 
– хорды кривой второго порядка, составляющие с ее осью одинаковые углы, и 
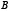является точкой пересечения этих хорд или лежащие на их продолжении, то для полученных при этом отрезков имеет место равенство 
.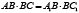