Как известно, отношение меры дуги к длине ее хорды, когда дуга неограниченно убывает, имеет предел, равный положительному числу. Доказательство этого предложения в геометрии Евклида известно, однако, понятие о дуге длины окружности имеет смысл и в абсолютной геометрии. Поэтому возникла задача провести доказательство указанного предложения без использования аксиомы параллельности.
Сначала докажем несколько вспомогательных предложений.
Предложение 1. Из отрезков, на которые биссектриса треугольника делит противоположную сторону, больше тот, который принадлежит большей стороне.
Пусть BC>AB. (Рис.1). Проведем медиану BS и продолжим ее на отрезке SD=BS, точку D соединим с точкой C. Очевидно,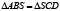 
и 
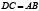, а следовательно, BC>DC и 
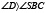. Но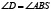 
, поэтому 
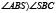, т.е. биссектриса угла 
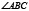пересекает сторону AC в некоторой точке K, лежащей между A и S, а так как AS=SC, то AK<KC.
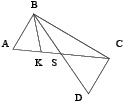
Рис. 1.
Предложение 2. Если в сумме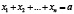 
положительных чисел слагаемые с возрастанием номера не убывают (возрастают) и сумма m первых слагаемых при m<n равна b, то
.
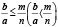Действительно, все числа, входящие в состав b, не больше каждого из чисел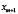 
,..., 
.,
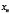Поэтому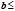 
, 
, ... , 
.
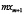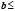
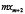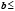
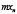складывая эти неравенства, получим
,
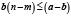откуда следует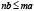 
, т.е. 
.
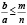В случае возрастания слагаемых аналогичные рассуждения дают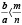 
.
Далее имеем следующие теоремы.
Теорема 1. Если дуга окружности неограниченно убывает, то отношение соответствующего ей отрезка касательной к ее хорде стремится к единице.
Пусть AB – хорда, стягивающая дугу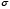 
, AC – соответствующей дуге отрезок касательной, O – центр дуги, AD – перпендикуляр, опущенный из точки A на OC (рис. 2).
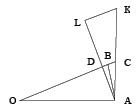
Рис. 2.
Так как лежит между C и D, то AD<AB<AC, а, следовательно,
.
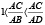На продолжении AC возьмем произвольную точку K и опустим из нее перпендикуляр KZ на прямую AD.
Так как по предыдущей лемме
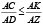, то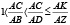 
.
Но при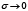 
последнее отношение стремится к 1,
поэтому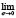 
.
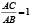Теорема 2. Предел отношения меры неограниченно убывающей дуги окружности к длине ее хорды существует и равен положительному числу.
В самом деле, если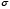 
– мера дуги, a – длина ее хорды и t – длина соответствующего дуге отрезка касательной, то
.
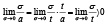Теорема 3. Существует система измерения дуг, при которой предел отношения меры неограниченно убывающей дуги к длине ее хорды равен 1.
Пусть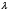 
– градусная мера и a – длина хорды дуги окружности и 
.
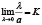Примем за единицу измерения дугу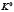 
. Новую меру дуги 
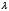обозначим через S. Так как новая единица в K раз больше старой, то
,
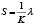а поэтому
.
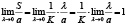Называя систему измерения, о которой говорится в последней теореме, линейной, а меру дуги в линейной системе измерения длиной дуги, получим следующую теорему.
Теорема 4. Длина всякой дуги окружности равна пределу, к которому стремится длина вписанной в дугу выпуклой ломаной, когда число звеньев ломаной неограниченно возрастает, так что каждая часть дуги, стягиваемая звеном, стремится к нулю.