Сетевое издание

Международный студенческий научный вестник

ISSN 2409-529X

Теория графов один из наиболее интересных разделов математики. Родоначальником теории графов считается швейцарский математик Леонард Эйлер, который в 1736 году сформулировал решение задачи о семи кёнигсбергских мостах, ставшей впоследствии классической задачей теории графов. Развитие этой теории долгое время не происходило, а лишь в середине 20 века интерес к проблемам теории графов вновь появился, главным образом в Англии. Наиболее известной задачей-проблемой того периода является задача четырех красок, которая была составлена математиком Огастесом де Морганом в 1850 году. В настоящее время теория графов неуклонно развивается и получил широкое распространение в экономических исследованиях. В последнее время все чаще наблюдается проникновение математики в разные сферы и отрасли многих наук. Этот процесс затронул и экономическую сферу. Для нахождения кратчайшего или объездного пути, рационального маршрута передвижения, для оптимизации производственного цикла применяется теория графов.

В экономической сфере задачи теории графов применяются для принятия локально оптимальных решений на каждом этапе, причем конечное решение также окажется оптимальным.

Классическим примером таких задач является практическое применение жадного алгоритма в решении экономических проблем.

Под жадным алгоритмом понимается алгоритм, основанный на жадной стратегии, то есть достижении конечного результата с наименьшими затратами.

Пусть на территории некоторого города N размещены заводы, которые поставляют свою продукцию в магазины. В результате разработки были определены возможные трассы для прокладки коммуникаций и оценена стоимость их создания для каждой трассы (табл. 1).

Необходимо, чтобы коммуникации связали все объекты, но затраты на прокладку данных коммуникаций должны быть минимальными (табл. 2).

Таблица 2

Обозначения объектов

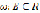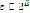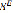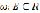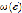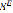Данная задача решается с помощью одной из разновидностей жадного алгоритма – алгоритма Краскала. Пусть имеется конечное множество E, при E = 18, весовая функция и семейство . Необходимо найти , такое что: E – конечное множество, – функция, ставящая в соответствие каждому элементу е этого множества неотрицательное действительное число – вес элемента . Для вес 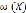определим как сумму всех элементов множества Х:

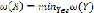
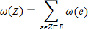
Необходимо выбрать в данном семействе непустое подмножество наименьшего веса. Сопоставив каждому пункту сети вершину графа , а каждому из ребер этого графа составить число, которое равно стоимости строительства соответствующей коммуникации. Согласно теореме, алгоритм Краскала всегда приводит к ребру, имеющему минимальный вес. То есть это ребро 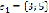, тогда получается граф 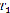. Строиться граф 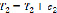, где 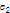– ребро, имеющее минимальный вес среди ребер, не входящих в 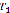и не составляющий циклов с ребрами , .

.

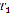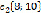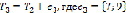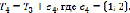
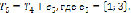
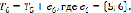
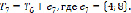
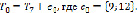
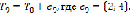
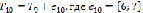
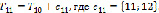
Найдено минимальное дерево покрытия взвешенного графа, а следовательно, найдена и оптимальная структура сети, где общая стоимость затраченная на прокладку коммуникаций составит:

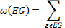10 + 15 + 2 × 20 + 4 × 25 + 3 × 30 = 255

Это минимальная сумма затрат из всех возможных исходов. При прокладке коммуникационной сети, которая соединяет все пункты, затрачивается 255 у.е.

Коммуникации необходимо проложить между следующими пунктами: аптека – кафе – завод №2 – хозяйственный магазин – завод №1 – пекарня – магазин канцтоваров – продуктовый магазин – текстильная фабрика – магазин №3 – торговый комплекс.

На основе вышеизложенного материала можно сделать вывод, что теория графов как один из разделов дискретной математики является многосторонним в применении, как в повседневной жизни человека, так и в других науках, в частности в экономике теория графов помогает решить проблему наиболее эффективного планирования процесса производства, а так же снижения транспортных издержек.