Одним из основных методов решения экономических задач является матричный метод. На данный момент особенно актуально использование матриц для создания баз данных, ведь вся информация обрабатывается и хранится в матричной форме.
Матрица – это прямоугольная таблица, представляющая собой совокупность строк и столбцов. Размерностью матрицы называется величина m×n, где m-число строк, n-число столбцов.
Впервые матрица появилась в Древнем Китае и носила название «волшебный квадрат». Чуть позже она стала известна и арабским математикам. В конце XVII века швейцарский ученый Габриэль Крамер разработал свою теорию, а в 1751 году опубликовал один из методов решения систем линейных уравнений «правило Крамера». Также в этот период был создан «метод Гаусса». Огромный вклад в развитие теории матриц в середине XIX внесли такие известные ученые как Уильям Гамильтон и Артур Кэли. Наряду с ними развивали данную теорию немецкие математики Карл Вейерштрасс и Фердинанд Георг Фробениус, а также, французский математик Мари Энмон Камиль Жордан. В 1850 году Джеймс Сильвестр ввел современное понятие матрицы.
Таким образом, в математике появился раздел, который называется матричной алгеброй. Матричная алгебра имеет очень важное значение в экономике. Обуславливается это тем, что матричный метод позволяет в достаточно простой и понятной форме записывать различные экономические процессы и объекты. Одним из примеров может послужить таблица распределения ресурсов по различным отраслям (табл. 1).
Таблица 1
Распределение ресурсов
|
Ресурсы |
Отрасли экономики |
||
|
Промышленость |
Сельское хозяйство |
Торговля |
|
|
Трудовые ресурсы |
4,8 |
6,7 |
7,1 |
|
Водные ресурсы |
3,1 |
2,5 |
5,8 |
|
Электро- энергия |
5,6 |
4,3 |
3,4 |
Данная таблица может быть записана в виде матрицы:
Так, например, элемент матрицы а22 = 25 показывает, сколько водных ресурсов потребляет сельское хозяйство, а элемент матрицы а13 = 7,1 показывает, сколько трудовых ресурсов потребляет торговля.
Другим примером может служить следующая задача:
предприятие выпускает три вида продукции С1, С2, С3 и на производство данной продукции использует два вида сырья К1, К2:
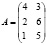
где каждый элемент аij показывает, сколько сырья j-того типа может быть израсходовано на производство продукции i-того типа. Стоимость каждого типа сырья задана матрицей-столбцом
,
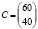а план выпуска продукции задан матрицей-строкой В = (90 130 50).
Таким образом, мы получим: затраты на сырьё
К1 = 4 × 90 + 2 × 130 + 1 × 50 = 670 (единиц),
а стоимость второго сырья
К2 = 3 × 90 + 6 × 130 + 5 × 50 = 1300 (единиц).
Следовательно, общая стоимость сырья
Р = 670 × 60 + 1300 × 40 = 92200 может быть записана в виде матрицы: Р = К × С = (ВА)С = 92200.
Отметим, что общую стоимость сырья P можно вычислить и в ином порядке: для начала, вычислим матрицу Z стоимостей затрат сырья:
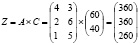
Общая стоимость сырья равна:
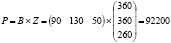
Одинаковость данных результатов (92200) получена благодаря выполнению ассоциативного закона произведения матриц: (ВА)С = В(АС)
Далее рассмотрим задачу:
В таблице 2 приведены данные о производительности 5 предприятий, которые выпускают 4 вида продукции с потреблением 3-х видов сырья, так же длительность работы всех предприятий в году и цена каждого вида сырья.
Таблица 2
|
Вид изделия № |
Производительность данных предприятий |
Затраты видов сырья изделия |
||||||
|
1 |
2 |
3 |
4 |
5 |
1 |
2 |
3 |
|
|
1 |
5 |
6 |
4 |
7 |
8 |
2 |
4 |
5 |
|
2 |
1 |
3 |
5 |
4 |
1 |
3 |
6 |
7 |
|
3 |
9 |
16 |
1 |
5 |
7 |
4 |
5 |
6 |
|
4 |
4 |
11 |
8 |
6 |
5 |
5 |
9 |
7 |
|
Количество полных рабочих дней в году |
Цена различных видов сырья |
|||||||
|
1 |
2 |
3 |
4 |
5 |
1 |
2 |
3 |
|
|
210 |
160 |
180 |
130 |
150 |
50 |
60 |
70 |
|
Необходимо определить:
1) Производительность каждого предприятия по каждому типу изделий;
2) Потребность каждого предприятия по каждому типу сырья;
3) Сумму кредитования предприятий для закупки сырья, которое необходимо для выпуска продукции указанных видов и количеств.
Решение задачи: составим матрицы, которые характеризуют весь экономический спектр производства. Построим матрицу производительности предприятий по всем типам продукции:
Каждый столбец данной матрицы соответствует производительности по каждому виду продукции. Исходя из этого, годовую производительность i-го предприятия по каждому виду продукции можно получить благодаря умножению i-го столбца матрицы C на количество рабочих дней в году для данного предприятия (i = 1, 2 ,3, 4, 5). Следовательно, годовую производительность каждого предприятия по каждому из изделий можно представить в виде матрицы:
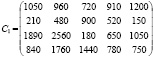
Матрица затрат сырья на единицу изделия (данные показатели по условию являются одинаковыми для всех предприятий) имеет следующий вид:
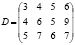
Расход по типам сырья на предприятиях можно описать при помощи произведения матрицы D на матрицу C:
где j-я строка соответствует номеру типа сырья, а i-й столбец – номеру предприятия согласно таблице (j =1, 2, 3; i =1, 2, 3, 4, 5).
На второй вопрос задачи ответ можно получить аналогично, умножив столбцы матрицы DС на соответствующее количество рабочих дней в году – это годовая потребность предприятий в каждом типе сырья:
Введем вектор стоимости сырья: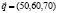 
Тогда стоимость годового запаса сырья для каждого предприятия получим путем умножения вектора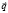 
на матрицу 
:
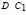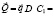
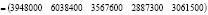
Исходя из этого, суммы кредитования предприятий для закупки сырья определяются соответствующими компонентами вектора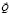 
.
Из вышеизложенного следует, что матрицы имеют ряд достоинств: позволяют в достаточно простой и понятной форме записывать различные экономические процессы и закономерности, дают возможность решать сложные задачи. Также с помощью матриц можно с минимальным количеством затрат труда и времени обработать большой статистический материал, различные данные, которые характеризуют структуру и особенности социально-экономического комплекса.