С помощью интегральных преобразований Фурье и Лапласа и матричного метода исследуется решения уравнений теории упругости для слоистой кубической системы в двумерной области. Получены асимптотические представления корней дисперсионных уравнений, удобные для численных расчетов на ЭВМ.
Рассмотрим в декартовой системе координат x, z систему из n-кубических слоев, ограниченных полупространствами. Во всех упомянутых средах плоскость изотропии параллельна границами раздела. При этом каждая среда описывается уравнениями Ляме
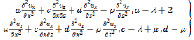(1)
и уравнениями закона Гука
; 
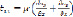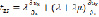(2)
в которых ρ – плотность;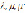 
– коэффициенты Ламе. На всех границах раздела имеют место условия жесткого контакта.
Uxi = Uyi + 1, Uzi = Uzi + 1, txzi = txzi + 1, tzzi =tzzi + 1, (3)
при которых непрерывны векторы смещений Ux, Uz, а также компоненты тензоры напряжения tzz, tzz. Поле смещений в заданной системе удовлетворяет нулевым начальным условиям
Ux/t=0 = 0, Uz/t=0 = 0,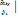 
t = 0 = 0, 
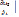t = 0 = 0, (4)
Пусть
φ1 = ux, φ2 = uz, φ3 = tkz, φ4 = tzz, f1 = -sinkx, f2 = coskx,
f3 = -ksinkx, f2 = kcoskx, F1 = Ux, F2 = Uz, F3 = Txz, Tu = Tzz (5)
величина η в общем случае характеризует фазовую скорость υ = │Imη│ и коэффициент затухания γ = R│Reη│ интерференционных волн, при этом k=2π/l – волновое число l – длина волны, а в случае нормальных волн η=iτ. Решения задачи с помощью интегральных преобразований
φi(x,z,t)=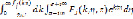
,
(j = 1,2,3,4) (6)
сводится к изучению системы дифференциальных уравнений
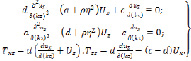(7)
Первым двум уравнениям (7) соответствует определяющее уравнение
adα4 – fα2 + (a + rη2)(d +rη2) = 0; (8)
α1,2 =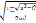 
; f = d(d +rη2)+d(d +rη2) c2 (9)
θ = 4dd(d + rη2)(d +rη2)
Выбор основной ветви радикала (9) и проведения разрезов из точек ветвления 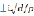η = 
и η =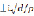 
проводится так же, как в [ I ].
Система (7) сводится к системе алгебраических уравнений. Решение последний системы запишем для каждого слоя и каждого полупространства рассматриваемой среды. Заданная системы возбуждается падающими из полупространств волнами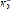 
, 
, 
, 
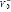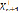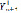которые представляются равенствами (6). Образующиеся в результате отражений и преломлений волновые поля удовлетворяют соотношениям (I), (2) и (4). Кроме того, эти поля совместно с падающими возмущениями удовлетворяют условиями (3). Для определения остальных 4(n+1) функций на основании (3) применяем обобщенный матричный метод [ I ].
А теперь исследуем дисперсионные уравнения, описывающие распространение нормальных волн типа в заданном слое при kh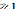 
. С математической точки зрения дисперсионное уравнение является характеристическим уравнением для собственных чисел некоторого дифференциального оператора, являющегося обобщением оператора Штурма- Лиувилля. В случае нормальных волн этот оператор является самосопряженным, а для затухающих-несамосопряженным.
Дисперсионное уравнение симметричного слоя относительно плоскости z = 0,5h разлагается на два уравнения.
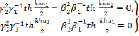(10)
Описывающие антисимметричные и симметричные колебания. Величины β1, γ1, β2, γ2 являются функциями от η, выражения которых получается из соответствующих выражения [ I ] при b=a d=m . Исследование уравнений проводится в областях
Tl – Im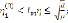
II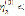 – Im
Im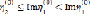
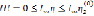
так же, как в [ 2 ].
При этом величины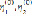 
являются точками ветвления внутреннего радикала (9) в верхней полуплоскости. Дисперсионные уравнения (10) при kh > 1 представляются соотношениями (11)
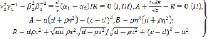
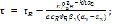
Уравнение Релея IR = 0 в данной области имеют один корень области (I) τ = τR. Если эта предельная точка лежит в области (I) получим представления 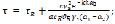(12)
(12)
а в случае τR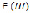
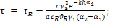
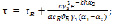(13)
(13)
Из этих равенств следует, что корни о разных сторон приближаются по экспоненциальному закону к предельной точке.
Если τR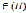
, то корни уравнений (10) имеют вид (14)
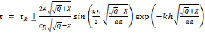
При этом в правых частях вместо величин A, θ, f имеем значения при τ = τR, а величина CR = dR/d(rτ2). Равенства (14) показывают, что корни приближаются к предельной точке, испытывая колебания около этой точки. Такой колебательной характер движения корней в области (II) является характерной особенностью дисперсионных уравнений анизотропной упругой среды.
Из вторых равенств (12) и (13), а также из монотонного характера перемещения особого корня симметричного дисперсионного уравнения следует, что скорость τR волны Релея, лежащая в интервалах (I) и (III) , удовлетворяют неравенству
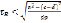(15)
Следует отметить, что используемые параметры a, c, d удовлетворяют условиям положительности плотности упругой энергии, а также неравенству, обеспечивающему однозначность определения скоростей распространения волн под любыми углами распространения [ 3 ]:
a + d – c > 0, a > d, d > 0; a(d – d) – c2 > 0 (16)
Наконец, отметим, что из-за ограниченности объема работы приведены только основные результаты исследований.