В последнее время в науке стало очень актуально изучать различного рода искусственно созданные тонкопленочные структуры, одномерные фотонные кристаллы на основе природных и специально сконструированных материалов. Такие структуры позволяют создавать всё новые и новые устройства фотоники, а также детали оптических компьютеров. Тонкослойные наноструктуры, составляющими которой являются металлы [3], диэлектрики, полупроводники [2], сверхпроводники [1], искусственные метаматериалы [7], обладают совершенно уникальными магнитоэлектрическими, механическими, теплофизическими и электродинамическими свойствами. Для того, чтобы управлять параметрами слоистых структур, в их состав необходимо включать материалы, свойства которых меняются под действием электрического и магнитного поля. Одними из таких материалов являются так называемые разбавленные магнитные полупроводники. А точнее – это соединения, получаемые при допировании немагнитных полупроводников небольшим количеством атомов переходных металлов (Sc, Ti, V, Cr, Mn, Fe, Co, Ni и Cu) [6].
Такие соединения ещё называют полупроводниковыми твёрдыми растворами, в которых основная диамагнитная кристаллическая решётка содержит некоторое количество парамагнитных примесных атомов. Концентрация примесных атомов не слишком велика, так что дипольное взаимодействие между их магнитными моментами мало. При этом расстояние между примесными атомами значительно больше постоянной решётки а, и они, в некотором приближении, подобны атомам идеального газа, с магнитной восприимчивостью χ, подчиняющимся закону Кюри. В роли магнитных примесных атомов могут выступать атомы переходных элементов, лантаноидов и актиноидов, имеющих нескомпенсированный электронный спин на f – или d – оболочках. Обменные эффекты при взаимодействии электронов проводимости или дырок с магнитными примесными атомами приводят к возможности магнитных фазовых превращений [4]. Подобными магнитными полупроводниками могут быть редкоземельные манганиты, керамика SiCN, активированная ионами переходных металлов, а также разбавленные полупроводники флюорита и рутила [6].
Манганиты и керамика проявляют большое разнообразие теплофизических свойств, но, к сожалению, имеют слишком высокую температуру перехода в ферроэлектрическое состояние с диапазоном температур порядка 600 – 900 К. А это нежелательное условие для вышеупомянутых структур, поэтому наибольший интерес представляют разбавленные полупроводники флюорита и рутила, имеющие температуру перехода порядка 300К. Эти разбавленные полупроводники в свою очередь, являются ферромагнетиками только в размере наночастиц при комнатной температуре. Структуры этих материалов представляют собой: соединение двуокиси церия CeO2 с никелем Ni или кобальтом Co (структура флюорита) и соединение окиси олова SnO2 с железом Fe, хромом Cr или кобальтом Co (структура рутила). Окись олова SnO2 – весьма привлекательный материал для широкого спектра практических приложений и является химически стабильным прозрачным оксидным полупроводником с широкой запрещенной зоной ~ 3.6 эВ. Было показано, что допирование кобальтом Co и железом Fe индуцирует ферромагнетизм в окиси олова SnO2, что позволяет рассматривать окись олова SnO2 как ферромагнитный полупроводник при комнатной температуре [8].
Рассмотрим магнитный полупроводник на основе окиси олова SnO2, допированный ионами Fe, имеющий формулу Sn1-xFexO2. Отжиг нанопорошка этого материала, в диапазоне температур TA ~ 350 – 600oC, приводит к резкому увеличению намагниченности насыщения [8]. В этом диапазоне температур происходит диффузия ионов Fe из ядра наночастицы к поверхности, и концентрация ионов Fe в поверхностной области увеличивается. Магнитный полупроводник на основе окиси олова SnO2 обладает сильными магнитными свойствами и является привлекательным материалом для создания устройств оптоэлектроники. Для расчета параметров таких устройств необходимо знать зависимость для намагниченности J от величины внешнего магнитного поля. Разбавленные магнитные полупроводники имеют очень сложный состав, и теория, описывающая их электродинамическое свойства в полном объеме, еще не создана. Для практического применения используем предложенную нами феноменологическую модель намагниченности и проведем аппроксимацию зависимости намагниченности J от магнитной индукции B с помощью формулы:
J = A ∙ ln(α ∙ B – β), (1)
где A, α и β – феноменологические константы. Приведем результаты аппроксимации намагниченности для разбавленного магнитного полупроводника Sn0.993Fe0.007O2 (см. рис.1). Экспериментальные данные для Sn0.993Fe0.007O2 приведены в работе [8]. Поиск феноменологических констант проводился по методу наименьших квадратов. В результате расчетов были найдены следующие значения: A = 0.83 ∙ 103А/м, α = 1.02 Тл-1, β = 0.97.
Из рисунка 1 видно, что предложенная феноменологическая зависимость (1) хорошо описывает экспериментальные данные, показанные на рисунке точками. Зная зависимость J от величины магнитного поля, можно рассчитать магнитную восприимчивость χ , которая связывает напряженность магнитного поля Н и усредненную намагниченность [5],
J = χ ∙ H , (2)
а также магнитную проницаемость
μ = χ + 1. (3)
Результаты расчетов магнитной проницаемости магнитного полупроводника Sn0.993Fe0.007O2 на основе предложенной феноменологической зависимости (1) показали хорошее соответствие с экспериментальными данными, приведенными в работе [8].
Выводы
В работе была предложена феноменологическая модель описания магнитных характеристик магнитного полупроводника. Для магнитного полупроводника на основе окиси олова, допированной железом, были найдены феноменологические константы, описывающие зависимость намагниченности разбавленного магнитного полупроводника от величины внешнего магнитного поля. Предложенную феноменологическую модель можно использовать для расчетов электродинамических параметров используемых в нанотехнологиях устройств на основе слоистых структур с разбавленными магнитными полупроводниками.
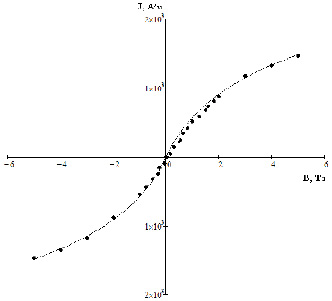
Рис. 1. Зависимость намагниченности разбавленного магнитного полупроводника Sn0.993Fe0.007O2 от магнитного поля. Точки – экспериментальные значения при Т=300 К (по данным [8]). Сплошная линия – результат аппроксимации по формуле (1)

