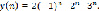Операционное исчисление играет важную роль при решении прикладных задач, особенно в современной автоматике. Обобщением обычного преобразования Лапласа на дискретные функции является дискретное преобразование Лапласа (Z – преобразование), которое является основным математическим аппаратом при анализе линейных импульсных систем.
Известно, что динамические процессы в дискретных системах управления описываются уравнениями в конечных разностях.
Решение линейных разностных уравнений с постоянными коэффициентами удобно проводить методом Z – преобразования, аналогично схеме применения преобразования Лапласа к решению задачи Коши для линейного дифференциального уравнения с постоянными коэффициентами. В результате применения этого метода к линейному разностному уравнению (или системе уравнений) с постоянными коэффициентами получаем уравнение (или систему уравнений) относительно изображения искомой ступенчатой функции, содержащее все начальные условия.
Пусть имеем комплекснозначную функцию f(t) действительного аргумента t, определенную для t≥0. Рассмотрим последовательность {f(n)} (n=0,1,2,…), которая обозначается f(n) и называется решетчатой функцией. Для отрицательных значений аргумента решетчатая функция равна нулю.
Решетчатая функция – это результат временного квантовая непрерывного сигнала, которая представляет значения непрерывного сигнала в дискретные моменты времени.
Дискретным преобразованием Лапласа (Z-преобразованием) решетчатой функции f(n) называется функция F*(p) комплексного аргумента p=S+iσ, определяемая равенством:
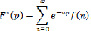 (1)
(1)
Предполагается, что ряд справа в (1) сходится. Функция f(n) называется дискретным оригиналом, а F*(p) – ее изображением и обозначается символом: F*(p)÷f(n) или f(n)÷F*(P).
Рассмотрим линейное неоднородное разностное уравнение:
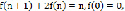 (2)
(2)
Решение задачи (2) будем искать операционным методом, основанном на дискретном преобразовании Лапласа. Применим Z-преобразование к обеим частям уравнения (2).
Пусть f(n)÷F*(p). Применяя теорему опережения, имеем:f(n+1)÷еᵖF*(p).
С учетом соотношения:
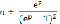
приходим к операторному уравнению:
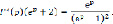
Отсюда находим изображение решения:
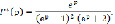 (3)
(3)
В случае, когда F*(p) есть правильная рациональная дробь относительно еᵖ, решетчатую функцию f(n) будем искать в виде:
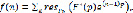 (4)
(4)
где сумма вычетов берется по всем полюсам функции F*(p), расположенным в полосе -π<Imp≤π и на ее границе Imp=π.
Функция F*(p) имеет один простой полюс: 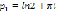 и один полюс
и один полюс 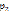 = 0 порядка 2 основной полосы -π<Imp≤π.
= 0 порядка 2 основной полосы -π<Imp≤π.
Находим вычеты функции F*(p)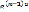 относительно полюсов
относительно полюсов 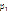 и
и 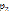 .
.
Так как 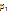 =ln2+πi – простой полюс, то (5):
=ln2+πi – простой полюс, то (5):
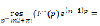
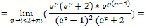
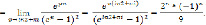
Поскольку 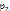 =0 – полюс порядка 2, то последовательно находим:
=0 – полюс порядка 2, то последовательно находим:
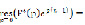
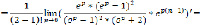
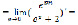
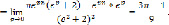 (6)
(6)
Таким образом, согласно формулам (4)-(6) искомая решетчатая функция принимает вид:
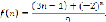
Далее рассмотрим следующую систему линейных разностных уравнений:
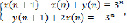 (7)
(7)
с начальными условиями:
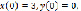 (8)
(8)
Применим Z-преобразование к системе (7)-(8). Пусть
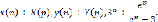 (8)
(8)
Согласно теореме опережения и условий (8) имеем:
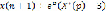 ,
,  .
.
Систему (7) - (8) запишем в операторном виде:
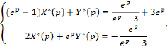 (9)
(9)
Будем решать систему (9) по правилу Крамера:
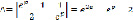
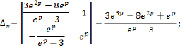
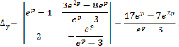
Отсюда находим решение системы (9)
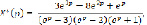 (10)
(10)
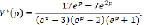 (11)
(11)
Теперь по изображениям X*(p) и Y*(p) будем восстанавливать решетчатые функции x(n) и y(n). Разлагаем дробь (10) на простейшие дроби. Имеем:
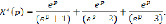 (12)
(12)
С учетом соотношений:
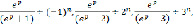
находим:
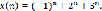
Решетчатую функцию y(n) будем искать с помощью формулы (9). Находим вычеты функции 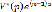 относительно полюсов
относительно полюсов  функции Y*(p). Так как полюсы
функции Y*(p). Так как полюсы 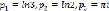 – простые, поэтому вычеты относительно этих полюсов принимают соответственно вид:
– простые, поэтому вычеты относительно этих полюсов принимают соответственно вид:
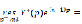
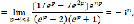 (13)
(13)
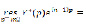
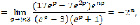 (14)
(14)
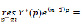
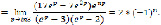 (15)
(15)
Объединяя формулы (9)-(11), получаем решетчатую функцию