Статистические закономерности являются фундаментальными законами природы. В работе [1] показано: идеальный график рангового распределения (РР) набора чисел случайных величин W (r) из Гауссового распределения представляет собой S-образную кривую, симметричную относительно биссектрисы прямого угла, образующего координатные оси W и r (рис.1). На рис.1,а представлено идеальное Гауссово частотное распределение fi = f (W ) и, соответствующее ему, РР этих же величин W(r) (рис.1, б).
График Гауссового распределения f (W) (рис 1, а) для наглядности повёрнут на 90 градусов в плоскости рисунка по отношению к графику рис. 1, б [1]. Приведённые графики являются результатом компьютерного моделирования случайных чисел (выборка 10000) с заданным Гауссовым распределением. Среднее значение случайной величины W = 200 (математическое ожидание) соответствует точке перегиба на S-образной кривой.
В методологии естественных наук известен способ определения принадлежности эмпирически полученного графика к той или иной математической зависимости. Этот метод идентификации заключается в построении полученной выборки эмпирических физических величин в «координатах спрямления» и приведения исследуемой функции к линейному виду в этих координатах. Этот метод широко используется физиками-экспериментаторами.
Представляет несомненную методологическую значимость нахождение координат спрямления для S-образной кривой РР случайных величин и применение этих координат с целью идентификации S-образного РР с вероятностным распределением случайных величин (Гауссовым распределением), что и составило цель исследования. Цель определила ряд конкретных задач и этапы исследования.
Этапы исследования.
1. Теоретическая часть:
• определение координат спрямления для S–образной кривой РР;
• нахождение и описание способа моделирования случайных чисел с заданным распределением вероятности;
2. Практическая часть:
• Проверка полученных теоретических результатов при помощи компьютерного модельного эксперимента.
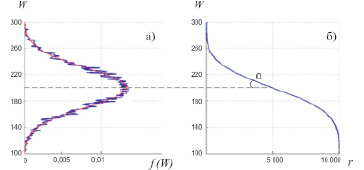
Рис. 1. а) Гауссово частотное распределение f i = f (W ) 10000 случайных величин со стандартным отклонением σ = 30, математическим ожиданием 200; б) соответствующее ему, РР этих же величин W (r) [1, с. 48].
Отметим, что S-образный вид эмпирического РР W (r) свидетельствует о принадлежности совокупности параметров W к Гауссовому распределению, при этом с уменьшением дисперсии Гауссового распределения крутизна S-образной характеристики РР увеличивается, угол α между касательной к S-кривой в точке перегиба и горизонтальной осью уменьшается [1].
В работах [2,3] показано, что математическая формула S-образной кривой имеет вид:
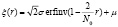(1)
где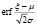 
– функция ошибок, или функция Лапласа [4, с.575], а 
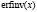– функция, обратная функции ошибок.
1) Нахождение координат спрямления для S-образ-ной кривой РР.
Чтобы найти координаты спрямления , нужно подставить (1) в функцию ошибок, при этом в координатах erf ξ (r) получается убывающая прямая:
erf {[ξ ( r ) – μ] / (√2 σ) }= а – (2 / N0) r = а – kr , (2)
где r – ранговый номер случайной величины ξ в порядке её убывания; а, k – постоянные, при этом k = 2/N0 отражает значение тангенса угла наклона прямой к оси рангов.
Проверка данного утверждения, осуществлённая при помощи компьютерного модельного эксперимента, описана ниже в п.3.
2) Моделирование случайных чисел с заданным распределением вероятности.
Ранее найден простой способ моделирования случайных чисел с заданным распределением вероятности. Известно, что:
,
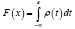где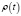 
– плотность вероятности. Свойством 
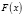является монотонность неубывающей функции, ограниченной в пределах от нуля до единицы, что очень кстати, так как любой язык программирования имеет генератор псевдослучайных чисел в интервале от нуля до единицы. Воспользуемся методом обратных функций.
Теорема. Пусть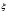 
случайная величина, равномерно распределенная на интервале 
, 
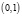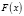– монотонная возрастающая функция на 
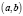, имеющая производную и пределы:
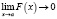и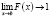 
Тогда существует обратная функция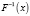 
, 
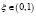и случайная величина 
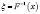распределена на интервале 
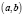с плотностью
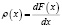[5].
Рассмотрим распределение Гаусса.
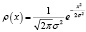(3)
Пусть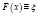 
, причем 
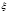– случайная величина, равномерно распределенная от нуля до единицы, тогда:
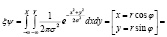
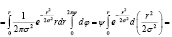
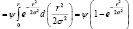(4)
где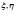 
– равномерно распределенные случайные величины в пределах от нуля до единицы.
Примем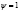 
и выразим r:
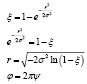(5)
В результате мы получаем две независимые случайные величины, распределенные по закону Гаусса из двух независимых равномерно распределенных случайных величин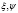 
:
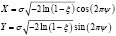(6)
Полученные формулы были запрограммированы в среде MatLab и были получены следующие эмпирические результаты.
3) Проверка полученных теоретических результатов при помощи компьютерного модельного эксперимента.
Были построены гистограммы Гауссовых распределений при различных значениях дисперсии (10,20,30,40,50) и, соответствующие им, S-образные кривые пузырьковым методом (ранжирование случайной величины по убыванию). Таким образом была проверена формула (2) (рис. 2, а, б)
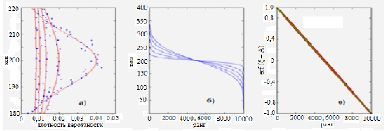
Рис. 2. К вопросу идентификации распределений случайных величин функции Гаусса (а); с S-образными РР (б, в)
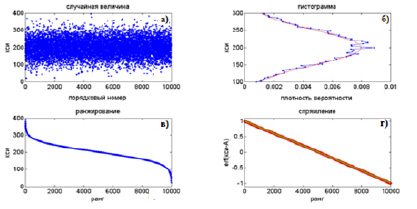
Дисперсия 50
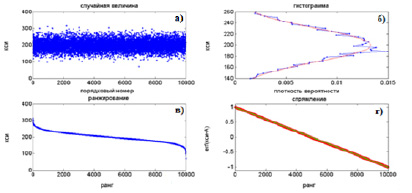
Дисперсия 30
Рис. 3. К вопросу спрямления функции Гаусса с разными дисперсиями: а) Поле случайных величин; б) Распределения Гаусса; в) Соответствующие им S-образные кривые РР; г) S-образные кривые РР в координатах спрямления
а) Гистограммы распределений случайных величин с дисперсиями 10,20,30,40,50. б) Соответствующие им S-образные кривые РР. в) Спрямление S-образных кривых РР в координатах erf (ξ – А) = f (r) (координатах спрямления).
Подобный алгоритм можно использовать для моделирования случайных величин, распределенных по необходимому закону. Ниже представлены рисунки (рис.3, а, б, в, г), иллюстрирующие описанный выше модельный эксперимент для двух дисперсий – 50 и 30.
Спрямление S-характеристики наглядно выглядит близким к идеальному случаю, когда все точки ложатся на кривую или попадают в доверительный интервал. В рассмотренных случаях моделирование доверительного интервала не предусмотрено, а большинство точек оказывается выше или ниже прямой, что обуславливает малое значение коэффициента регрессии.
Результаты исследования имеют теоретическую и практическую значимость, которая заключается в том, что ранговый анализ открывает новые возможности в методологии научных исследований, использующих построения нормальных распределений: по внешнему виду кривой РР в грубом приближении можно идентифицировать принадлежность выборки значений исследуемой величины к Гауссовому распределению.
Таким образом:
• Найдены координаты спрямления для S-образного РР случайных величин.
• Результаты модельного компьютерного эксперимента подтвердили спрямление S-образного РР в координатах erf ξ (r) , где ξ – функция ошибок, r – ранговый номер исследуемой случайной величины.
• Спрямление S-образного РР случайных величин в найденных координатах спрямления доказывает принадлежность исследуемой выборки случайных величин к вероятностному распределению Гаусса.
• Простота вышеизложенного метода – построение выборки случайных величин Гауссового распределения как S-образного рангового распределения и представление его в виде линейного графика в координатах спрямления позволяют сделать вывод о несомненной практической значимости проведённого исследования.
Результаты модельного компьютерного эксперимента подтверждены ранее проведённым натурным экспериментом по исследованию распределения числа импульсов от счетчика Гейгера-Мюллера [6].