Сетевое издание

Международный студенческий научный вестник

ISSN 2409-529X

Дифференциальное уравнение первого порядка ý = f(x, y) имеет общее решение 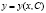, которое определяет собой семейство интегральных кривых на плоскости хОу.

Если переменные х и у правой части дифференциального уравнения рассматривать как координаты точки М(х, у) плоскости хОу, то производная 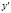выражает угловой коэффициент касательной к интегральной кривой в точке М(х, у). Таким образом, дифференциальное уравнение ý = f(x, y) определяет в каждой точке плоскости хОу, принадлежащей области существования функции , направление интегральной кривой, проходящей через эту точку, или определяет поле направлений на плоскости хОу.

Изображая направление в каждой точке области существования функции 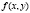маленькой стрелкой, выходящей из этой точки, можно построить поле направлений дифференциального уравнения, которое дает приближенное представление о расположении интегральных кривых этого уравнения.

Изоклинами дифференциального уравнения ý = f(x, y) называются геометрические места точек плоскости хОу, в которых интегральные кривые уравнения имеют одно и то же направление. Уравнение 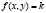является уравнением изоклины, соответствующей заданному направлению 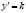, где 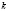– параметр. Придавая 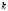близкие числовые значения, получается достаточно густая сеть изоклин – семейство изоклин, с помощью которых можно приближенно построить интегральные кривые дифференциального уравнения. Нулевая изоклина 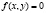дает уравнение линий, на которых могут находиться точки максимума и минимума интегральных кривых. Точки пересечения двух или нескольких изоклин могут быть особыми точками дифференциального уравнения, т.е. такими точками, в которых правая часть уравнения ý = f(x, y) не определена.

Метод изоклин состоит в следующем:

1. Строится достаточно густая сетка изоклин для различных значений k и на каждой изоклине изображаются небольшие отрезки с наклоном k.

2. Начиная из точки (x₀, y₀), поводится линия, которая, будет пересекать каждую изоклину под углом, заданным полем направлений. Полученная таким образом кривая и будет приближенным изображением (эскизом) интегральной кривой уравнения, проходящей через точку (x₀, y₀).

Пусть дано уравнение 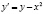и требуется построить поле направлений и интегральные кривые, определяемые этим уравнением.

Сначала строятся графики изоклин. Уравнение семейства изоклин данного уравнения 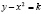или 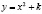. Изоклины представляют собой семейство квадратичных парабол с осями, совпадающими с осью Ох. Меняя параметр k, получается семейство графиков изоклин, на них строится поле направлений.

При k=0 получается изоклина 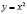, во всех точках которой направление поля параллельно оси Ох (Рис. 1).

При k=1 получается изоклина 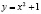, во всех точках которой направление поля образует с осью Ох угол .

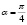При k=-1 получается изоклина 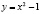, во всех точках которой направление поля образует с осью Ох угол .

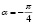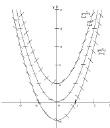
Рис. 1. Поле направлений уравнения .

Задается определенная точка (x₀, y₀) и поводится линия, которая, будет пересекать каждую изоклину под углом, заданным полем направлений. На рис. 2 показаны интегральные кривые, касающиеся поля направлений.

Метод изоклин как метод приближенного решения задачи Коши устарел. В его в основе лежит алгоритм изображения фрагмента поля направления, а современные компьютеры могут мгновенно и как угодно подробно нарисовать поле направлений, и достаточно точно изобразить интегральную кривую.

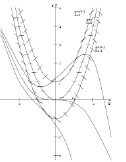
Рис. 2. Интегральные кривые уравнения .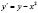

Однако, метод изоклин эффективно работает как инструмент исследования поведения решений. Он позволяет изобразить области характерного поведения интегральных кривых и как средство эскизного представления интегральных кривых сохраняет свое значение и в нынешнюю эпоху бурного развития вычислительных машин и вычислительных методов.