Согласно проведенным исследованиям в настоящее время очень актуальным является изучение взаимодействия α-частиц и нуклонов с ядром 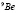 для разнообразных приложений, в частности для проблемы управляемого термоядерного синтеза и в атомной технике. В работе описано исследование мультикластерной (2α+n)-модели ядра
для разнообразных приложений, в частности для проблемы управляемого термоядерного синтеза и в атомной технике. В работе описано исследование мультикластерной (2α+n)-модели ядра 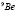 с вычислением его статистических характеристик.
с вычислением его статистических характеристик.
Трехчастичная (2α+n)-модель ядра 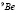
Для описания ядра 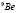 используется трехчастичная модель 2α+n (см.рис.1) с тремя парными αn и αα – взаимодействиями, включающими состояния, запрещенные принципом Паули.
используется трехчастичная модель 2α+n (см.рис.1) с тремя парными αn и αα – взаимодействиями, включающими состояния, запрещенные принципом Паули.
Волновая функция ядра 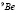
Базисная волновая функция относительно координат Якоби (см.рис.1) [1]:
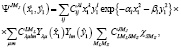 (1)
(1)
где 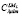 ,
, 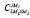 – коэффициенты Клебша-Гордана;
– коэффициенты Клебша-Гордана;
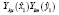 – сферические функции относительных координат;
– сферические функции относительных координат;
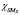 – спиновая функция системы;
– спиновая функция системы;
λ, l – относительные орбитальные моменты ( в координатах Якоби);
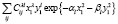 – радиальная часть волновой функции ( Гауссоида).
– радиальная часть волновой функции ( Гауссоида).
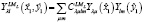 (2)
(2)
Формула (2) выражает угловую часть волновой функции (1).
Волновая функция допускает чисто алгебраическую пересвязку к другому набору координат Якоби. В частности, преобразование радиально-угловой части базисной волновой функции (1) от набора 1 к набору 2 (см.рис.1) имеет вид:
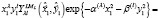
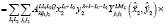
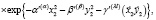 (3)
(3)
где алгебраический коэффициент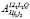 определяется по формуле:
определяется по формуле:
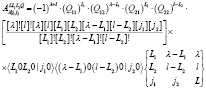
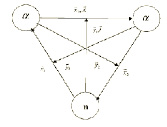
Рис.1. Выбор наборов внутренних координат Якоби.
Статистические характеристики
В данном параграфе мы покажем выводы статических характеристик основного состояния для ядра 9Be в трехтельной модели, для чего сначала выразим все операторы, записанные в одночастичных координатах, через относительные координаты, – координаты Якоби.
Среднеквадратичный зарядовый радиус
Среднеквадратичный зарядовый радиус 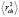 определяется следующим выражением [2]:
определяется следующим выражением [2]:
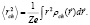 (4)
(4)
Здесь Ze- заряд ядра. Одночастичная зарядовая плотность 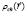 имеет следующий вид:
имеет следующий вид:
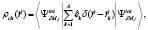
Для вычисления 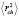 в
в 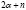 – модели нужно перейти от одночастичных координат
– модели нужно перейти от одночастичных координат 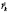 к новым:
к новым:
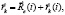 (5)
(5)
где 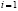 для
для 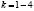 и
и 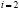 для
для 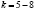 .
. 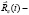 координаты центра масс частицы относительно всего ядра,
координаты центра масс частицы относительно всего ядра, 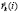 – координаты k-го нуклона частицы относительно ее центра масс. Координаты центра масс частиц выражаются через координаты:
– координаты k-го нуклона частицы относительно ее центра масс. Координаты центра масс частиц выражаются через координаты:
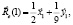
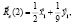
После несложных вычислений для 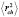 получим
получим
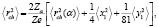 (6)
(6)
где матричные элементы для и могут быть легко найдены:
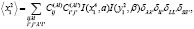
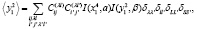
Здесь использованы следующие обозначения для радиальных интегралов:
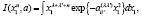
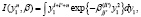

Магнитный момент
Оператор магнитного момента 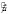 системы состоящей из трех частиц, имеет вид [2]:
системы состоящей из трех частиц, имеет вид [2]:
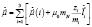 ,
,
где 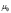 – ядерный магнетон Бора,
– ядерный магнетон Бора, 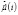 – оператор внутреннего магнитного момента
– оператор внутреннего магнитного момента  -й частицы,
-й частицы, 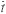 – оператор орбитального момента
– оператор орбитального момента  -й частицы массой
-й частицы массой 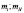 - масса нуклона. Перейдем от моментов
- масса нуклона. Перейдем от моментов 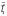 к моментам
к моментам 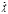 и
и 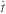 :
:
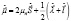 (7)
(7)
Перепишем выражение (7) для 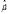 в другом виде, для простоты опустим знак оператора
в другом виде, для простоты опустим знак оператора  :
:
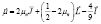
Магнитным моментом ядра  называется величина :
называется величина :
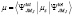 .
.
При расчете магнитного момента воспользуемся следующей формулой:
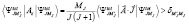 ,
,
а также 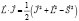 .
.
Учтя это, мы получим 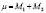 , где
, где
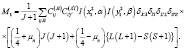 (8)
(8)
Член 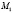 можно представить через веса
можно представить через веса 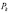 компонент
компонент 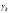 :
:
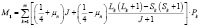 ,
,
где  – число учитываемых конфигураций. А второй член выражении для магнитного момента равен:
– число учитываемых конфигураций. А второй член выражении для магнитного момента равен:
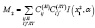 ×
×
×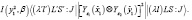
Квадрупольный момент
Квадрупольный момент ядра 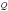 определяется следующем выражением[2]:
определяется следующем выражением[2]:
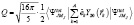 , (9)
, (9)
где 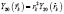 – пространственная сферическая гармоника. Снова переходя от одночастичных координат
– пространственная сферическая гармоника. Снова переходя от одночастичных координат 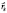 к новым, согласно соотношению
к новым, согласно соотношению 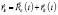 и используя следующую формулу (10):
и используя следующую формулу (10):
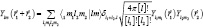 ,
,
получаем:
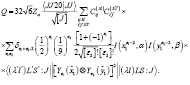 (11)
(11)
В формуле (11) для приведенного матричного элемента использованы стандартные обозначения.
Октупольный момент
Октупольный момент ядра 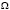 называется величина [2]:
называется величина [2]:
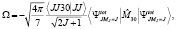 (12)
(12)
где 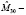 оператор октупольного момента – состоит из двух частей:
оператор октупольного момента – состоит из двух частей:
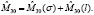
Спиновая часть оператора октупольного момента
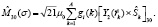
Здесь 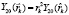 – пространственная сферическая гармоника, ядерный магнетон Бора. Спиновое гиромагнитное соотношение равно:
– пространственная сферическая гармоника, ядерный магнетон Бора. Спиновое гиромагнитное соотношение равно:

Орбитальная часть оператора октупольного момента:
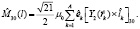
Матричный элемент от спиновой части равен:
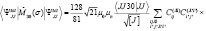
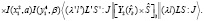
Орбитальную часть матричного элемента от оператора преобразуем к виду
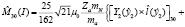
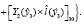
Волновая функция (1) допускает чисто алгебраическую пересвязку к другому набору координат Якоби, что мы и используем при расчете матричного элемента от орбитальной части оператора октупольного момента. При преобразовании функции от набора координат 1 к набору 2 (см.рис.1), где двумерная гауссоида преобразуется:
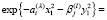
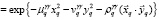
Аналогичным образом преобразуется гауссоида
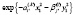 .
.
Для того чтобы исключить перекрестный член 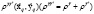 в экспоненте, совершаем еще одно преобразование координат Якоби. В результате этого преобразования получаем:
в экспоненте, совершаем еще одно преобразование координат Якоби. В результате этого преобразования получаем:
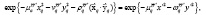
Учитывая формулы для матричного элемента от орбитальной части оператора, получаем:
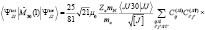
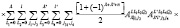
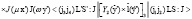 ,
,
где радиальные интегралы 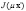 и
и 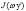 равны:
равны:
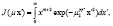
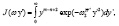
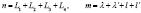 .
.

