Сетевое издание

Международный студенческий научный вестник

ISSN 2409-529X

1. Введение

Исследование электрических цепей, находящихся в магнитной связи, приводит к решению обыкновенных дифференциальных уравнений высших порядков. Эти уравнения встречаются в задачах электродинамики и в ряде других разделов физики (см. напр., [1]). Теория этих уравнений в настоящее время хорошо разработана.

Ниже рассматриваются два связанных электрических контура, исследование которых приводит к решению дифференциального уравнения четвертого порядка.

2. Постановка задачи и описание алгоритма

Рассматриваются две цепи A и B, находящиеся в магнитной связи при заданном коэффициенте М = 2 взаимной индукции (см. рис. 1).

Дано: коэффициент самоиндукции L₁ = 2 млГн, сопротивление R₁ = 150 Ом и емкость цепи «А» C₁ = 15 мкФ; L₂ = 3 млГн, R₂ = 200 Ом и C₂ = 10 мкФ – аналогичные величины для цепи «В».

Найти закон изменения силы тока i в цепи A, предполагая, что сопротивления цепей R₁ и R₂ весьма малы; цепи настроены в унисон, т.е. C₁L₁=C₂L₂.

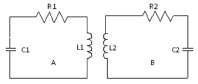
Рис. 1

При составлении уравнений для токов в электрических цепях используется второй закон Кирхгофа: алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме электродвижущих сил (ЭДС), входящих в этот контур.

В цепи A возникают силы: ЭДС индукции 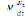, ЭДС самоиндукции 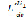, напряжение конденсатора .

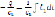Отсюда по закону равновесия электродвижущих сил имеем

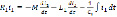(1)

Аналогично для цепи B получаем

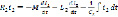(2)

Из уравнений (1) и (2) составляем систему дифференциальных уравнений процесса

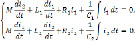
После дифференцирования имеем

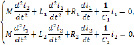(3)

Эта система двух дифференциальных уравнений второго порядка. Исключим из системы (3) величину .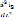

Тогда получим выражение

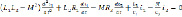(4)

Дифференцируя уравнение (4), находим

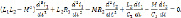(5)

В уравнении (5) заменяем величину 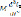выражением из первого уравнения системы (3)

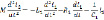
и получаем соотношение

Дифференцируя уравнение (6), находим

Вторично заменяя величину 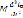выражением из первого уравнения системы (3), получим

.

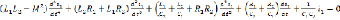Сокращаем уравнение (7) на :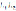

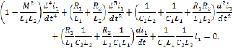
Так как цепи настроены в унисон, т. е. 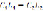, и сопротивлениями R₁ и R₂ можно пренебречь, то уравнение (8) принимает вид

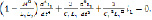
3. Численная реализация

Различают точные и приближенные методы решения дифференциальных уравнений. Несмотря на то, что большое количество уравнений может быть решено аналитическим способом, часто требуется найти числовое значение при определенных исходных данных. Поэтому широкое распространение получили численные методы, которые реализуются функциями «MathCAD». Для решения однородного дифференциального уравнения четвертого порядка применим такие функции, как Given и Odesolve. Как известно, функция Odesolve возвращает решение дифференциальных уравнений, описанных в блоке Given при заданных начальных условиях.

Ниже приводятся программы, реализующие решение поставленной задачи (8), (9).

В первой программе активные сопротивления ничтожно малы, поэтому ими можно пренебречь (9):

Given

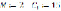
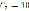
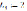
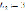
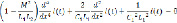
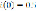
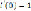
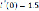
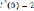
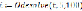
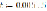
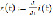
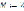
i(t)=

Для сравнения, рассмотрим случай, когда учитываются активные сопротивления (8):

Given

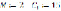
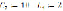
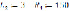
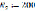
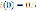
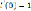
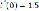
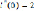
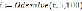
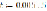
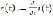
i(t) =

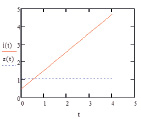
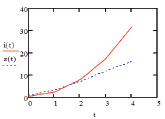
Если сравнивать полученные результаты из двух программ, можно сделать следующий вывод: в первом случае, когда активные сопротивления пренебрежительно малы, величина тока значительна и наблюдается экспоненциальный рост. Во втором случае, когда ток зависит от сопротивления, просматривается линейное возрастание .

С помощью проведенных вычислений нашли зависимость тока от сопротивления в цепи: чем больше сопротивление в цепи, тем меньше ток.