Возможные пути решения проблемы подготовки высококвалифицированного специалиста заключаются в совместном использовании, по крайней мере, двух категорий процесса обучения: модульно-рейтинговой системы организации учебного процесса; формирования мотивации к самообучению при организации практикума нетрадиционной формы.
Работа выполнена в формате курсового проектирования для образовательных программ бакалавриата технических направлений.
Цель работы: проверка разработанной нами ранее методологии модельно-математического исследования технических систем [1].
Динамический анализ позволяет произвести полный силовой расчёт технического объекта с целью определения законов движения его звеньев под действием заданных сил.
В работе исследуется многомассовая механическая система с одной степенью свободы, представленная в учебнике [2]. Составим уравнения движения системы в форме уравнения Лагранжа 2-го рода. В качестве обобщённой координаты принят угол поворота ведущего звена φ.
Вычисляем кинетическую энергии многомассовой механической системы реального объекта.
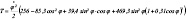 (1)
(1)
Обобщенная сила системы равна:
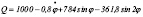 (2)
(2)
Уравнения (1) и (2) решены в среде математического пакета MathCad 14 методом Рунге-Кутта.
Изменение энергосиловых характеристик системы представлены на рисунке. Например, величина кинетической энергии механической системы Т зависит от угловой скорости ведущего звена и не зависит от направления движения точки D (точка подвеса штанг). Величина обобщенной силы Q отличается по модулю на 30% для различных перемещений точки D.
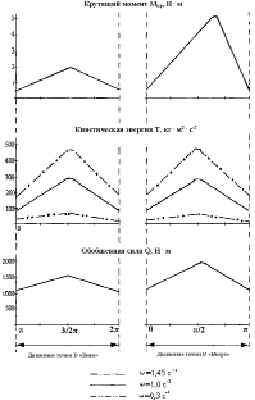
Изменение энергосиловых параметров системы за время равное полному обороту ведущего звена
Модуль крутящего момента меняется в зависимости от направления движения точки D.Для хода точки D вниз: увеличение модуля крутящего момента носит линейный характер (см. рисунок).
Для хода точки D вверх: модуль крутящего момента увеличивается до 2,5 раз; изменение его носит скачкообразный характер (рисунок),
Модуль крутящего момента пропорционален величине углового ускорения ε1 и тангенциальной составляющей суммарного усилия Fτ на пальце ведущего звена (точка А).
Подтверждается известное положение [2], что силовое взаимодействие в точке D отличается по величине при ходе точки D «вверх» и «вниз» на 30-50%. Дисбаланс активных сил при ходе «вниз» заставляет механическую систему в целом дополнительно «разгонять» приводной электродвигатель, переведя его на работу в «генераторном» режиме.
Выводы.
1. Предложенная методология модельно-математического мышления, использована для формирования учебно-исследовательской компетентности обучающихся на примере исследования динамики механической системы.
2. Применение данной методологии требует от обучающегося умения пользоваться специальной технической литературы и позволяет ему самостоятельно получить углубленные знания и навыки, развивающие его творческие способности.

