Исследуя свойства прогрессирующих матриц, авторы выявили достаточно интересные факты – равенство нулю определителей матриц, составленных из последовательных членов арифметической и геометрической прогрессий ([1]), последовательности чисел Фибоначчи, а также некоторых других последовательностей (числа Леонардо, числа Люка, последовательность Падована) ([2]).
Были проанализированы доступные литературные источники, среди которых «Введение в теорию матриц» Р.Беллман ([3]), «Курс высшей алгебры» А.Г.Курош ([4]), интернет-источники ([5], [6]). Выяснилось, что указанный выше результат ни в одном из источников не представлен. Знание же указанного факта, да и ещё полученного с помощью собственных теоретических изысканий, имеет первостепенное значение для студента с методической точки зрения, не говоря о том, что указанное свойство само по себе важно для математики.
Поэтому изучение вопроса о прогрессирующих последовательностях и квадратных матрицах (и их определителях), составленных из последовательных членов этих последовательностей, является актуальным.
Основные цели исследования заключаются в выявлении свойств прогрессирующих последовательностей; определении класса последовательностей, обладающих аналогичными свойствами; определении значимости найденных свойств, их применения. Задачами исследования являются выявление свойств арифметических и геометрических прогрессий, чисел Фибоначчи, члены которых последовательно заносятся в квадратные матрицы соответствующих размеров; устойчивость свойств при соответствующих изменениях в последовательности заносимых элементов в матрицы.
Объектами исследования выступают числовые последовательности с заданными законами их получения, квадратные матрицы различных порядков, в которые заносятся последовательно члены последовательностей, их определители.
Предметом исследования являются свойства числовых последовательностей, а, именно, значение определителей, получаемых из последовательных членов числовых последовательностей.
Для того чтобы провести исследование подобное данному, необходимо владеть навыками интеллектуальной деятельности, уметь сопоставлять, обобщать, анализировать и делать самостоятельные выводы. Поэтому применены следующие методы исследования: анализ научно-методической литературы по теме, индукция и дедукция, анализ и синтез, сравнение, обобщение, эксперимент, в частности компьютерный эксперимент.
Авторами сразу же было установлено, что свойство – равенство нулю значения определителя матрицы, составленной из членов любой геометрической прогрессии, имеет место по основным свойствам определителей (пропорциональность по строкам и/или столбцам).
Далее рассматривались свойства арифметических прогрессий. Задав с помощью программы ([1]) b := f1(3, 3, 25) матрицу, получаем определитель 0 (рис. 1).

Рис. 1. Вычисление по программе (функция пользователя) определителя 5-го порядка для членов арифметической прогрессии
Изменим в приведённой выше матрице, к примеру, элементы второго столбца на произвольные числа (рис. 2 а)), аналогично – элементы третьей строки (рис. 2 б)).
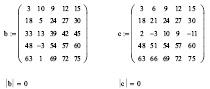
а б
Рис. 2. Значение определителя матрицы с элементами, состоящими из двадцати пяти членов арифметической последовательности: а – 2-й столбец заменили произвольными числами, б – 3-я строка заменена произвольными числами
Проверим, может быть имеется пропорциональность по строкам или столбцам указанных матриц (рис. 3).

Очевидно, что пропорциональность не наблюдается (!), поэтому делаем вывод о том, что в подобных матрицах имеются более глубокие зависимости. На результат не повлияло изменение («порча») столбца, строки матрицы.
Аналогичный эффект наблюдается и для матриц, содержание которых – последовательные значения чисел Фибоначчи. Пусть имеется матрица пятого порядка, состоящая из последовательных чисел Фибоначчи, начиная с третьего члена (рис. 4).


Рис. 4. Значение определителя матрицы с элементами, состоящими из двадцати пяти членов последовательности Фибоначчи, первый элемент матрицы является третьим членом последовательности
Произведём следующие изменения с матрицей j (рис. 4): элементы второго столбца заменим произвольными числами (случай а) рис. 5); элементы третьей строки также произвольными числами (рис. 5 б)).

а

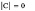
Рис. 5. Значение определителя матрицы с элементами, состоящими из двадцати пяти членов последовательности чисел Фибоначчи: а – 2-й столбец заменили произвольными числами, б – 3-я строка заменена произвольными числами
Очевидно, что изменения квадратных матриц, составленных из элементов арифметических и геометрических прогрессий, а также последовательности чисел Фибоначчи, построчно или по столбцам не влияют на их вырожденность, т.е. значение определителя остаётся равным 0. Указанное свойство назовём помехоустойчивостью матриц, составленных из членов прогрессирующих последовательностей (или проще – помехоустойчивостью прогрессирующих последовательностей) и последовательности чисел Фибоначчи.
Возможности использования введённого нового понятия – помехоустойчивости прогрессирующих последовательностей – на практике:
– может быть использовано для передачи больших объёмов информации в двумерных виде массивов с контролем потерь при передаче;
– для криптозащиты передаваемой информации.

