В настоящее время наблюдается противоречие между увеличением числа часов, отводимых на самостоятельную проработку обязательного учебного материала, и недостаточной разработанностью моделей, описывающих эффективную самостоятельную работу и тем более способствующих ее оптимизировать.
Проблема исследования – разработка методологии модельно-математического мышления комплексного исследования технических систем.
Цель исследования – создание обучающих документов, способных оптимизировать процессы изучения и модернизации реальных технических систем.
В данной работе областью исследования является содержательный компонент обучения. Интеграция содержания образования это результат взаимодействия его структурных элементов: формы организации, методы и средства обучения и воспитания, определяющийся ростом системности и уплотненности знаний [1]. Базовым признаком системы знаний, которая может быть построена с использованием содержательным компонента является интегральная целостность [1].
В качестве объекта исследования выбрана реальная многомассовая техническая система с одной степенью свободы [2]. Методика исследования реализует уровни подготовленности специалиста-бакалавра [3].
Актуальность исследования: наличие дисбаланса активных сил приложенных к механической системе за время, равное полному обороту ведущего звена, который вызывает перерасход энергии приводного электродвигателя и повышенный износ деталей системы:
Снижение дисбаланса активных сил может достигаться различными способами уравновешивания, которые должны обеспечивать равенство максимальных значений крутящего момента (равенство работ) за полный цикл работы системы (перемещение точки D «вверх» и «вниз». Суммарные нагрузки при перемещениях точки D могут отличаться от 30÷ 50%.
Экспериментально доказано [2], что степень неуравновешенности механической системы может быть оценена величиной
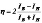 (1)
(1)
где IB и IH – ток статора электродвигателя при ходе «вверх» и «вниз» соответственно. Соблюдение этого условия подтверждается с помощью теории Д. Максвелла об электромеханических аналогиях в системе «сила-ток».
Вычислительный эксперимент проведён в пакете MathCAD 14. Получены графики изменений угла поворота φ и кинематических параметров (рисунок).
Движение точки D (точка подвеса штанг) вверх ω=1с-1
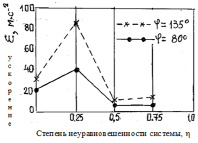
Движение точки D (точка подвеса штанг) вниз ω=1с-1
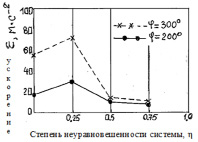
Зависимость модуля углового ускорения ε от степени неуравновешенности системы
Анализируя результаты вычислительного эксперимента, подтверждается, что установка дополнительных противовесов существенно влияет на величину внутренних кинематических параметров w и ε для исследуемых перемещений точки D (рисунок). Предполагаем, что степень неуравновешенности механической системы применительно к её конструктивному исполнению может быть оценена: 0,25 – балансирное уравновешивание, 0,5 – роторное уравновешивание, 0,75 – комбинированное уравновешивание, 1,0 – теоретически возможное уравновешивание. Неуравновешенная система имеет степень неуравновешенности – 0.
Выводы:
1. Средой для реализации предложенных форм и средств изложения материала является, как правило, комплексные темы с применением компьютерных и инновационных технологий.
2. Интеграция содержания отдельных дисциплин естественнонаучного цикла зависит от степени разработанности теоретической базы, реализующей профессиональную направленность каждой дисциплины или ее основных разделов.
3. Создание обучающимися электронных образовательных документов способствуют активизации исследовательской деятельности обучающихся.

