В курсе высшей математики, читаемом в вузе, встречается много имен знаменитых математиков (в названиях теорем, правил, формул и др.), которые не всегда знакомы студентам и которые преподаватель зачастую оставляет без внимания. При этом упускается возможность повысить познавательный, методический, эмоциональный уровень преподавания.
Исторические же сведения, умело преподнесенные на занятиях по математике, выполняют много функций:
Образовательная функция исторического материала по математике заключается:
- в углублении знаний по математике;
- в совершенствовании знаний и умений;
- в систематизации и обобщении полученных знаний;
- в расширении умственного кругозора студентов, исторические сведения помогают уточнить содержание рассматриваемого вопроса в прошлом и настоящем, сделать традиционные знания более ясными, точными и продуктивными.
Развивающая функция исторического материала служит развитию:
- дедуктивного мышления;
- способностей абстрагировать, обобщать, систематизировать и составлять суждения;
- находить пути решения поставленной задачи;
- математической и литературной речи, творческих способностей, воображения и самостоятельности. Исторические сведения способствуют широте, целенаправленности, оригинальности мышления.
Воспитательная функция состоит:
- в повышении общей культуры студентов;
- в привитии навыков самостоятельной работы;
- в понимании роли математики в современном обществе. Воспитывает способности отстаивать свои взгляды и убеждения, способствует воспитанию настойчивости в достижении поставленной цели.
При изложении исторического материала можно различать такие взаимосвязанные компоненты, как:
- биографические сведения об известных математиках, представленные в подробной или краткой форме;
- история развития идей, теорий, решения отдельных задач;
- история возникновения отдельных математических понятий, терминов, обозначений;
- анализ ошибок математиков прошлого.
Любой преподаватель, безусловно, может самостоятельно решить, биографиям каких математиков следует уделить больше внимания, какие детали и яркие моменты в их деятельности важно подчеркнуть. Это зависит от эрудиции, научных интересов преподавателя; времени, отведенного для чтения курса; уровня подготовки студентов. Различными могут быть и формы обращения к истории математики: сообщение или небольшой экскурс преподавателя, подготовка доклада или реферата студентами, оформление стенгазеты, стенда, публикация в студенческой газете, организация математического конкурса. Бесспорно воспитательное значение знакомства с биографиями великих математиков. Как правило, это люди, которые упорно трудились, сталкивались с непониманием своих идей и методов, испытывали зачастую материальные лишения. Они проявляли целеустремленность при решении своих задач, были честны и корректны при получении научных результатов. Для молодого поколения представляют интерес и политические взгляды ученых. Как правило, математики, преданные науке, не обнаруживали склонности к занятиям политикой (И.Ньютон, К.Ф.Гаусс и др.), хотя многие из них жили во времена революций и войн. Примером может служить жизнь и деятельность Пьера Симона Лапласа (1749-1827), который упоминается в связи с изучением функции Лапласа, оператора Лапласа и др. Математик, астроном, философ, он занимал одно время даже пост министра в правительстве Наполеона. Его политические убеждения менялись вместе с формами правления во Франции. В ранней молодости мы застаем его республиканцем, потом он сблизился с Наполеоном и по милости первого консула был очень короткое время министром внутренних дел, затем занимал место сенатора. К счастью для него и для науки, он как нельзя лучше воспользовался своим положением для упорного труда, поглощавшего все его время. В то время, когда Лаплас шел своим гладким путем, другие ученые переживали различные трудности. Возьмем, например, Гаспара Монжа (1746-1818) с именем которого мы встречаемся в геометрии [4].
В 1789 году вспыхнула революция; во всей Франции заговорили о справедливости, свободе и равенстве; в пылкой душе Монжа, также гениального математика, зашевелились воспоминания о несправедливостях и унижении. Монж с сильным душевным волнением ожидал минуты, когда призовут его к участию в общем движении. 12 февраля 1793 года Монж, однако, оставил свою общественную деятельность. Он лично любил Наполеона, но это не мешало ему стоять за правду. Когда Наполеон стремился превратить республику в империю, воспитанники Политехнической школы открыто порицали действия первого консула. В то время, как Наполеон сделался императором, те же воспитанники отказались приносить ему поздравления. С этого времени Наполеон возненавидел Политехникум; он хотел наказать зачинщиков, но Монж смело выступил их защитником. Наполеон сказал Монжу: «Однако твои политехники открыто воюют со мною». – «Государь, - отвечал Монж, - мы долго старались сделать их республиканцами, дайте им, по крайней мере, время превратиться в империалистов. Вы поворачиваете слишком круто» [1].
Мы приводим в пример чуткость и независимость современника Лапласа, математика Монжа, для того, чтобы показать, что не наукой, а личными качествами Лапласа обусловливалось его отношение к окружающей действительности. Революция не нарушила его покоя, не остановила его работ; напротив, в эту эпоху он начал самое капитальное свое сочинение, “Небесную механику”, которое закончил во времена реставрации. Когда Наполеон стал императором, он возвысил Лапласа в графское достоинство и произвел в рыцари Почетного легиона. Но все милости, оказанные Наполеоном Лапласу, нисколько не расположили к нему последнего; в 1814 году Лаплас открыто выражал свою преданность Бурбонам. Бурбоны тоже не остались у него в долгу; Людовик XVIII сделал его пэром и возвел в звание маркиза. С тех пор Лаплас сделался роялистом. При каждом удобном случае он доказывал это на деле и даже подал голос за закон против свободы печати. Французская академия, в которой он состоял президентом, решила протестовать против закона; Лаплас отказался от этого и мотивировал свой отказ тем, что в академии не должно быть места политике. Никто и не считал Лапласа серьезным политическим деятелем. Сам Лаплас видел в политике лишь создание себе безопасного и во всех отношениях выгодного положения.
Непростыми были взаимоотношения Жана Батиста Жозефа Фурье (1768-1830) с режимом Наполеона. И все-таки некоторые математики, как правило молодые, отдали дань политической борьбе. Деятельность Б.Паскаля была направлена против ордена иезуитов. Существует версия, будто дуэль, на которой погиб Э. Галуа, была устроена его политическими противниками [2].
Исторические сведения можно преподносить с различной степенью полноты. Недостаток времени на занятиях зачастую не позволяет подробно излагать биографии всех математиков, имена которых встречаются в курсе. Обычно можно ограничиться несколькими наиболее значительными и яркими деталями. Тем не менее, представляется уместным после выведения формулы Ньютона-Лейбница остановиться на жизни и деятельности Исаака Ньютона (1642-1727) и Готфрида Вильгельма Лейбница (1646-1716), их взаимоотношениях, связанных с соответствующим периодом (что и делает наш преподаватель Головина Ольга Владимировна). В публикации 1686 г. Лейбниц ввел знак интеграла, который представляет собой вытянутую букву S – первую букву латинского слова summa, отметив взаимную обратимость операторов ∫ и d. Символы и термины Лейбница (дифференциал, дифференциальное исчисление, функция, координаты, дифференциальное уравнение, алгоритм) оказались очень удачными. Они были несложными и отражали существо дела, помогали пониманию и позволяли оперировать ими по сравнительно простым правилам. Для Лейбница интеграл был суммой бесконечного числа слагаемых – определенный интеграл в современном понимании. Для Ньютона интеграл представлялся как семейство первообразных – неопределенный интеграл. Крайне неприятные приоритетные споры об открытии математического анализа развернулись в 17 веке между Ньютоном и Лейбницем. Формально они окончились победой Ньютона, не претерпевшего в результате их ни малейшего материального или морального ущерба, тогда как Лейбниц из-за споров умер буквально в нищете. Однако исторически победителем оказался именно Лейбниц. Вся континентальная Европа восприняла дифференциальное и интегральной исчисление в том обличье, которое придал ему Лейбниц [6]. Выдающийся советский математик Александр Яковлевич Хинчин (1894-1959) [1], рассказывая студентам Московского университета о значении формулы Ньютона - Лейбница, являющейся, по его словам, «жемчужиной» математики, обязательно делал исторический экскурс. Затем он отпускал студентов домой раньше времени, чтобы они запомнили как праздник день знакомства с замечательной формулой, связывающей воедино все дифференциальное и интегральное исчисление. Интересна и поучительна биография великого французского математика, механика, литератора Жана Лерона Даламбера (1717-1783), который упоминается в теме «Ряды» (признак Даламбера). Подкидыш, воспитанный бедными людьми, преодолевший жизненные трудности, лишения, он сумел стать одним из самых знаменитых людей мира. Достаточно сказать, что все статьи физико-математического цикла «Энциклопедии» Д. Дидро, оказавшей огромное влияние на поколение, совершившее Великую французскую революцию, написаны Даламбером.
Также можно рассказать о жизни и научной деятельности самых молодых выдающихся математиков: норвежце Нильсе Генрихе Абеле (1802-1829), который упоминается при изложении темы «Ряды» (теорема Абеля), и французе Эваристе Галуа (1811-1832). Непонимание со стороны известных математиков, нужда, которую терпел Абель, и политическая борьба Галуа против королевской власти в сочетании с полученными ими результатами, касающимися невозможности решения произвольного алгебраического уравнения выше четвертой степени, должны заинтересовать студентов.
Сведения по истории математики могут излагаться в форме вкраплений в материал, что удобно при недостатке времени. Примером такой подачи материала может служить упоминание о семье Бернулли. Большой вклад в математику внесли три представителя этого большого семейства базельских ученых XVIII в.: Якоб, Иоганн I и Даниил. Якоб (1654-1705) многими своими работами способствовал созданию теории вероятностей одна из основных математических моделей для описания независимых повторений опытов, используемых в теории вероятностей. Его брат, Иоганн I (1667-1748) вывел так называемое правило Лопиталя. Сын Иоганна I, Даниил (1700-1782), ввел (вместе с Л.Эйлером) в математику «второй замечательный предел». Интересно, что дифференциальное уравнение Бернулли было составлено старшим братом, Якобом, а решено младшим – Иоганном I.В письме Лейбницу 4 сентября 1696 г. И. Бернулли показал, что «уравнение Бернулли»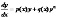 
сводится заменой 
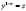к линейному. Из письма Лейбницу в том же году следует, что И. Бернулли проинтегрировал уравнение 
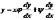, называемое теперь уравнением Лагранжа. В «Математических лекциях о методе интегралов и о других вопросах, написанных для маркиза Лопиталя» решено однородное уравнение 
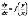подстановкой у=хt. Сделав на одном из занятий небольшое сообщение о семье Бернулли общего характера, можно возвращаться к ее представителям при рассмотрении интегрального исчисления, теории рядов, их применении к интегрированию, а также для решения практических задач. Роль И. Бернулли как одного из создателей, распространителей и, бесспорно, знатоков зарождавшегося тогда математического анализа отражает современная терминология: название «интегральное исчисление» (от латинского integer – целый, откуда и старинное русское «целоственный анализ») ввел И. Бернулли. Он занимался приложением рядов к интегрированию и на этом пути открыл общую формулу разложения в ряд интеграла от функции n(z) по степеням аргумента:
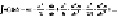
До сих пор в учебной литературе находит себе место парадокс И. Бернулли [4]. Запишем таблицу: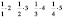 
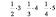
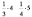
Просуммировав по строкам, найдем
S1 =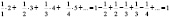 
,
S2 =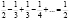 
S3 =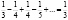
…………………………………….
Обозначим сумму строк буквой S: S=S1+S2+S3+…=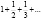
Просуммируем теперь столбцы и сложив результаты; получим
σ1=1/2, σ2=1/3, σ3=1/4, …; σ1+σ2+σ3 + … =1/2+1/3+1/4+ ... = S-1
Получается парадокс: S=S-1. Все объясняется просто: мы оперируем с расходящимся гармоническим рядом, не имеющим суммы.
Назрела необходимость собрать воедино и систематизировать методы дифференциального и интегрального исчислений с тем, чтобы ими мог пользоваться более широкий круг людей. Эту задачу блестяще выполнил И. Бернулли, написавший в 1691-1692 гг. «Лекции по исчислению дифференциалов» и «Математические лекции о методе интегралов и других вопросах, написанные для маркиза Лопиталя» [5]. Завершение лекций дало возможность писать И. Бернулли в автобиографической заметке, что он «был первым, кто подумал об изобретении метода для перехода от бесконечно малых количеств к конечным, элементами которых эти бесконечно малые суть. Я назвал этот метод интегральным исчислением, не найдя более подходящего слова».
Дифференциальное и интегральное исчисления возникли в связи с необходимостью решать конкретные механические и геометрические задачи, не поддававшиеся средневековой и античной математике. А ряды? Они на первый взгляд кажутся крайне искусственными, но это глубокое заблуждение. Ряды возникли одновременно с дифференциальным и интегральным исчислениями, и теория их строилась Ньютоном, Лейбницем, представителями семьи Бернулли и последующими математиками. С рядами дело обстояло так же естественно, как и с другими важнейшими разделами математики, получившими бурное развитие в XVIII в.: они применялись там, где другие средства исследования отказывали. Степенные ряды давали возможность приближенно решать уравнения, вычислять значения функций, вычислять интегралы, не выражающиеся через конечное число элементарных функций, решать дифференциальные уравнения, не интегрируемые в конечном виде. Много замечательных имен встречается при изложении темы «Ряды»: Ж.Л. Даламбер, О.Л. Коши, Г.В. Лейбниц, П.Г. Дирихле, Н. Абель, Б. Тейлор, Б.Ж. Фурье и др [6]. Преподаватель может посвятить им обзорный доклад или поручить это сделать студентам. Обычно приходится характеризовать деятельность каждого ученого лишь несколькими фразами.
История математики связана не только с крупными учеными. Сохранилось имя Шевалье де Мере, интересовавшегося математикой (в частности теорией азартных игр), который обратился с вопросами к гениальному ученому Блезу Паскалю (1623-1662). Имя последнего известно студентам больше из курса физики (закон Паскаля, гектопаскали) [3]. Проблемы, поставленные шевалье де Мере, носят его имя и иногда называются «задача о разделе ставки» и «задача о наилучшей стратегии выигрыша». Паскаль помог решить обе задачи, заложив тем самым основы теории вероятностей и комбинаторики. В дальнейшем обе науки стали развиваться с учетом потребностей страхового дела, статистики народонаселения, необходимости создания методов обработки результатов наблюдений. С развитием теории вероятностей и комбинаторного анализа связано много имен известных ученых (П. Ферма, Г.В. Лейбниц, Я. Бернулли, Л. Эйлер, П.Л. Чебышев и др.).
При изложении многих тем полезно сообщать о возникновении различных терминов, обозначений. Так, знакомя с теорией дифференциального и интегрального исчислений трудно не упомянуть о терминологии Лейбница, введенных им символах интеграла и производной, которыми мы пользуемся постоянно. Ряд задач такого рода был решен математиками Древней Греции. Античная математика предвосхитила идеи интегрального исчисления в значительно большей степени, чем дифференциального. Большую роль при решении таких задач играл исчерпывания метод созданный Евдоксом Книдским [1] и широко применявшийся Архимедом. Однако Архимед не выделил общего содержания интеграционных приёмов и понятия об интеграле, а тем более не создал алгоритма интегрального исчисления. Учёные Среднего и Ближнего Востока в 9-15 вв. изучали и переводили труды Архимеда на общедоступный в их среде арабский язык, но существенно новых результатов в интегральном исчислении они не получили. Деятельность европейских учёных в это время была ещё более скромной. Лишь в 16 и 17 вв. развитие естественных наук поставило перед математикой Европы ряд новых задач, в частности задачи на нахождения квадратур, кубатур и определение центров тяжести. Труды Архимеда, впервые изданные в 1544 (на латинском и греческом языках), стали привлекать широкое внимание, и их изучение явилось одним из важнейших отправных пунктов дальнейшего развития интегрального исчисления. В итоге этих исследований выявилась общность приёмов интегрирования при решении внешне несходных задач геометрии и механики, приводившихся к квадратурам как к геометрическому эквиваленту определённого интеграла. Заключительным звеном в цепи открытий этого периода было установление взаимно обратной связи между задачами на проведение касательной и на квадратуры, т. е. между дифференцированием и интегрированием. Дальнейшее развитие интегрального исчисления в 18 в. связано с именами И. Бернулли и особенно Л. Эйлера. В начале 19 в. интегральное исчисление вместе с дифференциальным исчислением было перестроено О. Коши на основе теории пределов. В развитии интегрального исчисления в 19 в. приняли участие русские математики М. В. Остроградский, В.Я. Буняковский, П.Л. Чебышев. В конце 19 - начале 20 вв. развитие теории множеств и теории функций действительного переменного привело к углублению и обобщению основных понятий интегрального исчисления.
Совсем немного времени отнимает, например, сообщение о том, что знакочередующийся ряд:
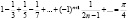
Называется рядом Лейбница, а число е названо по первой букве великого Леонарда Эйлера (1707-1783) [3]. Начиная с Декарта появилась традиция именовать постоянные первыми буквами латинского алфавита (а,b,с,...), а переменные - последними (x, y, z,...). Особо выделим методический прием, основанный на использовании ошибок как самих студентов, так и некоторых математиков. Например, иногда студенты ищут производную произведения как произведение производных, что является неверным: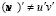 
На самом деле справедлива формула: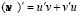 
Если сообщить студентам, что первоначально также ошибались Ньютон и Лейбниц, то это положительно повлияет на их эмоциональное состояние и позволит лучше запомнить правильную формулу. На ошибках великих учиться не обидно и даже приятно.
При изучении числовых рядов полезно привести пример ряда частичные суммы которого равны попеременно то 0, то 1. Еще в XVIII в. некоторые ученые полагали, что сумма ряда равна среднему арифметическому этих чисел, т.е. 1/2. Этот парадокс связан с недостаточным развитием в то время теории рядов. После введения строгих понятий сходимости, суммы ряда считается, что рассматриваемый ряд расходится, т.е. вообще не имеет суммы. Студентам демонстрируется преимущество владения развитым теоретическим знанием. Иногда допустимо напоминать студентам, что тот или иной материал был известен уже древним грекам или арабам. Так, если забыты основы школьной алгебры и при переносе выражения в другую часть уравнения не меняется знак, то уместно, указав на ошибку, упомянуть Муххамеда бен Мусса аль Хорезми (VIII-IX вв.), назвавшего это действие «аль-джебр», от чего и произошло наименование «алгебра», имя же самого ученого дало термин «алгоритм».
Исторические сведения хорошо воспринимаются, помогают им запомнить материал, пробуждают интерес к истории науки, заставляет преподавателя искать новые сведения, изучать историческую литературу, подбирать темы для самостоятельной работы студентов.