Человек обладает определенным объемом математических знаний; все умеют считать и отличать треугольник от квадрата, цилиндр от шара и конуса. Но не каждый понимает, что площадь правильного треугольника [квадрата] всегда будет больше площади прямоугольного треугольника [прямоугольника, трапеции], имеющего с ним одинаковый периметр. Этот факт можно выделить процентным отношением площади S1 египетского треугольника со сторонами 3,4,5, имеющего периметр 12, и площади S2 правильного треугольника со стороной 4. Поэтому первым примером математического процента будет сопоставление: S1/S2=6/4√3=3/2√3=√3/2≈0,866=86,6 %. Вторым примером на вычисление периметров правильного треугольника и равновеликого египетскому: a2√3/4=6; a2√3=24; a2=8√3=>a=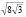
, P1=3
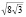≈11,16; P1/P2=11,16/12=93%.
Ответы разные, что соответствует трудности понимания принципа двойственности (или взаимности) двух взаимосвязанных задач оптимизации. Вычисление периметра оказалось довольно сложным, требующим использования микрокалькулятора или двукратного применения таблицы квадратных корней.
Математика, в отличие от других областей знаний, имеет возможность экономной и быстрой проверки на истинность. Для этого нужно не просто подобрать «хорошие» числовые параметры, но и создать арифметические математические теории. Наиболее древней является теория пифагоровых треугольников, созданная шумерской и китайской цивилизациями. Формулы пифагоровых триад: a=p∙q; b=(p2−q2)/2; c=(p2+q2)/2, где p,q – нечетные числа. В заданиях ОГЭ в каждом варианте используется египетская триада 3,4,5 и одна из трех: 8,15,17; 7,24,25; 5,12,13, причём не только в примерах, где по условию задан треугольник, но и в трапециях и, даже, в параллелограммах.
Знание общей формулы триад не просто упорядочивает, а усиливает само понимание математики.
Но и здесь важна идея системности: треугольник со сторонами 8,15,17 близок к чертежному треугольнику с углами 30о,60о,90о, которые составляют арифметическую прогрессию 30о:60о:90о=1:2:3. Естественно, возникает вопрос: существуют ли другие примеры с заданными свойствами.
Такой пример есть, этот треугольник интересен тем, что треугольник A1B1C1 образованный основаниями высот AA1, BB1, СС1 является «полуправильным» с углами 30о,60о,90о. На рисунке 1 углы A,B,C,A1,B1,C1 равны соответственно 45о,60о,75о,90о,60о,30о.
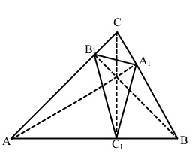
Рис. 1
Между этими треугольниками существует сложная взаимность. Впишем в полуправильный треугольник A1B1C1(С2B1A2) окружность и опустим из центра перпендикуляры на катеты и гипотенузу. Основания этих перпендикулярных радиусов образуют треугольник A3B3C3 подобный треугольнику АВС (рис. 2).
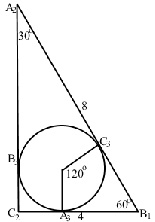
Рис. 2
Длины сторон полуправильного треугольника нельзя задать только рациональными числами. Пусть a=4, b=4√3, c=8. Отношения сторон пропорциональны a:b:c=1:√3:2. Радиус окружности, вписанной в полуправильный треугольник, равен r=(a+b−c)/2=4∙(1+√3−2)/2=2∙(√3−1)≈1,464.