Сетевое издание

Международный студенческий научный вестник

ISSN 2409-529X

Заработная плата имеет фундаментальное значение для экономических отношений, поэтому она является предметом изучения многих выдающихся ученых. На протяжении очень длительного периода в истории ученые пытались определить разнообразные факторы, влияющие на процесс трудовых отношений и на основе данных факторов сформировать теорию оплаты труда, которая была бы универсальной. На различных исторических этапах развития общества было свое видение этой проблемы.

Практически все экономические школы в своих научных работах, в той или иной степени, затрагивали проблемы формирования и распределения доходов в обществе. Основоположники экономической науки: У. Пети, Д. Рикардо, А. Смита (теория «Минимума средств существования»), рассматривали в своих трудах общеметодологические и общетеоретические основы исследования природы заработной платы. К. Маркс рассматривал заработную плату как результат стоимости рабочей силы. Саму сущность заработной платы рассматривали в своих трудах, такие знаменитые ученые, как Т. Мальтус (теория «Фонда заработной платы»), Ж.Б. Сей, А. Маршалл (теория «предельной производительности»), Й. Шумпетер, Дж. Хикс. Говоря о современных условиях теории заработной платы, то наибольшее внимание в своих работах, ей уделяют К.Р. Макконнелла, C.Л. Брю (учебник «Экономикс»), а также лауреат Нобелевской премии по экономике за 1972 год, Кеннет Джозеф Эрроу.

Почему же данный вопрос заслуживает столько внимания? Ответ прост: заработная плата имеет огромное значение в развитии экономики государства, подъеме благосостояния общества. Чем выше уровень заработной платы, тем более процветающей и развитой становится экономика, тем меньше социальных проблем. Необходимо отметить, что она является основным источником улучшения экономического благосостояния рабочих и служащих, а с другой, – стимулом роста и совершенствования производства. Очевидно, что материально заинтересованные работники в результатах своего труда, способствуют непрерывному развитию и совершенствованию процесса создания товаров и услуг.

Так, например, Правительство Российской Федерации ставит перед собой следующие цели на долгосрочное развитие:

• «распространение механизмов социального партнерства, обеспечение сбалансированности заработной платы и производительности труда» [7];

• «создание эффективных рабочих мест и рост заработной платы ежегодный рост заработной платы в 2011 – 2020 годах составит 7,6-9,7 процента, в целом в экономике к 2020 году она возрастет по сравнению с 2007 годом в 3,3 раза» [7];

• «до 2020 года будет обеспечено постепенное сближение среднего размера оплаты труда работников бюджетной сферы с размерами заработной платы, сложившимися во внебюджетном секторе экономики» [7];

• «в структуре доходов населения предусматривается повышение доли заработной платы с 37,6 процента в 2007 году до 42,4 процента в 2020 году» [7].

По данным Росстата, среднемесячная номинальная начисленная заработная плата в расчете на одного работника в Российская Федерация в среднем по всем отраслям за 2012 год составила «26628,9 рублей» [8]. Насколько достоверно и полно данная цифра отражает уровень развития российской экономики и зарплаты в целом по России? Следует учесть, что Российская Федерация состоит из 85 субъектов, разных по численности населения, площади, а также по экономической активности. Для понимания ситуации поверхностного взгляда недостаточно: сводные данные по всей стране не дадут представления о региональных особенностях, нужен более детальный анализ. Необходимость такого анализа обуславливает актуальность данной работы, рассматривающей проблему с применением эконометрических методов.

Целью моего творческого задания является определение степени влияния определенных факторов на среднемесячную номинальную начисленную заработную плату работников в среднем по всем отраслям экономики (рублей) (Y). По-моему, наиболее актуальной темой сегодня является реформирование Пенсионного фонда Российской Федерации, поэтому я считаю необходимым рассмотреть влияние средней назначенной пенсии, в месяц (X1) и численность занятых в экономике, приходящихся на одного пенсионера (в среднем за год (человек)) (X2). Говоря о заработной плате, мы непосредственно говорим о доходах населения, следовательно, для более точного влияния факторов необходимо рассмотреть потребительские расходы в среднем на душу населения, в месяц (рублей) (X3). Безусловно, численность экономически активного населения (тыс.чел.) (X4) также напрямую влияет на плату за труд, ведь чем вышел численность экономически активного населения, тем, при прочих равных условиях, производство больше. Также в современной социально-экономической политике Российской Федерации большое внимание уделяется такому явлению, как безработица, поэтому анализ влияния уровня безработицы (%) (X5), также является одной из приоритетных целей моей работы. Бесспорно, рассматривая заработную плату того или иного региона, необходимо учитывать уровень экономической активности населения (%)(X6), так как он непосредственно влияет на величину зарплаты.

Основными источниками данных для исследования послужили Федеральная служба государственной статистики [9] и Министерство финансов Российской Федерации [10]. Представлена информация по вышеперечисленным факторам по 50 субъектам Российской Федерации на 2012 год.

Анализ влияния факторов на среднемесячную номинальную начисленную заработную плату

В первую очередь решается вопрос о включении факторов в модель регрессии. Данный шаг можно выполнить тремя способами: 1) пошаговый отбор методом исключения; 2) на основе визуального анализа матрицы коэффициентов парной корреляции; 3) тест Фаррара-Глоубера.

Целесообразнее начать с пошагового отбора методом исключения. Для него необходимо использовать инструмент «Регрессия» (Данные ->Анализ данных -> Регрессия). Необходимо оценить значимость коэффициента регрессии с помощью критерия Стьюдента (табличное значение критерия Стьюдента равно: tтабл (α = 0,01; df = n – k – 1 = 10)) [3]. Сравнивая численные значения критериев, если tрасч.< tтабл. (означает, что коэффициент регрессии незначим при вероятности 99%). Пошагово исключаем из модели факторы, имеющие по модулю значение критерия Стьюдента (Вычисляем повторно с новыми данными, до момента, когда мы не можем больше исключить ни один из факторов).

В результате пошагово метода получается следующее уравнение регрессии:

Y= -34391,56 + 3,646 × X₁ + 10751,783 × X₂ + 0,464 × X₃

Данное уравнение имеет следующее экономическое значение: при увеличении назначенной пенсии на 1 рубль, средняя заработная плата увеличивается примерно на 3,65 рубля. При увеличении численности занятых в экономике, приходящихся на одного пенсионера на 1 человека, средняя заработная плата увеличится на 10751,78 рублей. При увеличении потребительских расходов в среднем на душу населения на 1 рубль, средняя заработная плата увеличивается примерно на 0,46 рублей.

Теперь вычислим уравнение регрессии на основе визуального анализа матрицы коэффициентов парной корреляции. Влияние объясняющих переменных на результирующий фактор можно проверить с помощью оценки коэффициента корреляции (Данные,-> Анализ данных -> Корреляция) (таблица 1).

Исходя из визуального анализа, целесообразнее всего исключить факторы X₄ и X₅, так как их коэффициенты корреляции с Y незначительны.

Проведя регрессионный анализ, получаем следующее уравнение регрессии:

Y = -29031,6 + 3,775 × X₁ + 11246,359 × X₂ + + 0,475 × X₃ – 109,912 × X₆

Вывод: увеличение назначенной пенсии на 1 рубль => увеличение заработной платы на 3,76 рубля; увеличение численности занятых в экономике, приходящихся на одного пенсионера на 1 человека, средняя заработная плата увеличится на 11246,36 рублей; увеличение потребительских расходов в среднем на душу населения на 1 рубль, средняя заработная плата увеличивается примерно на 0,475 рублей; увеличение уровня экономической активности населения на 1% уменьшает среднюю заработную плату на 109,91 рублей.

Последним способом является тест Фаррара-Глоубера. В основе данного метода лежит проверка мультиколлинеарности всего массива переменных.

FGнабл = 129,2863

FGкрит = 24,9958

Так как FGнабл > FGкрит (129,2863> 24,9958), то в массиве объясняющих переменных существует мультиколлинеарность.

Второй шаг данного метода заключается в следующем: проверка наличия мультиколлинеарности каждой переменной с другими переменными. Так как F1(19.98), F2(7.89), F3(7.86), F4(5.18), F5(5.08), F6(20.72) > Fтабл.(2,32), то независимые переменные Х1, X2, X3, X4, X5 и Х6 мультиколлинеарны с другими.

Третьим шагом является проверка наличия мультикллинеарности каждой пары переменных. Необходимо вычислить t-критерии по формуле:

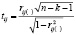
Для этого необходимо вычислить коэффициенты корреляции по формуле:

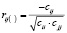
где c_jj – элементы матрицы C.

Таблица 1

Коэффициенты корреляции

Сравниваем данные t-критерии с критерием Стьюдента и исключаем те переменные, где t-критерий меньше критерия Стьюдента (учитывая Fкрит.).

В итоге получаем уравнение регрессии:

Y= -33739,1 + 25734,72X2 + 1,263095X3 – 216,108X5

Вывод: увеличение численности занятых в экономике, приходящихся на одного пенсионера на 1 человека, средняя заработная плата увеличится на 25734,72 рублей; увеличение потребительских расходов в среднем на душу населения на 1 рубль, средняя заработная плата увеличивается примерно на 1,26 рублей, увеличение уровня безработица приводит к снижению заработной платы примерно на 216,12 рублей.

Учитывая проведенные мной расчеты, по-моему мнению, наиболее точно с экономической точки зрения данная модель описана в первом случае, поэтому дальнейшем в работе я буду оперировать уравнение регрессии полученным пошаговым отбором методом исключения.

Далее необходимо оценить качество построенной модели.

R = 0,973879499

Коэффициент множественной корреляции показывает высокую тесноту связи зависимой переменной Y с тремя включенными в модель объясняющими факторами

R-квадрат = 0,948441278

Коэффициент детерминации показывает, что около 95% вариации зависимых переменных учтены в модели и обусловлено влиянием включенных факторов. Так как близок к 1, то качество модели высокое.

Точность модели оценим с помощью средней ошибки аппроксимации:

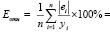7,44.

Чем меньше рассеяние эмпирических точек вокруг теоретической линии регрессии, тем меньше средняя ошибка аппроксимации; Еотн. < 7% свидетельствует о хорошем качестве модели.

Проверка значимости:

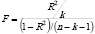= 282,0621953.

Вывод: при данном уровне значимости (a=0,05) F расч. > F табл.(2,80684494), значит модель является значимой.

Далее необходимо проверить адекватность построенной модели. Нам необходимо подтвердить или опровергнуть гипотезу:

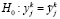
1) Имеющаяся выборка делится на две неравные части. Первая объемом 5-10% от общего объема выборки, вторая – все остальное. Первую выборку называют контрольной, вторую – обучающей.

2) По обучающей выборке вновь проводится идентификация модели.

3) Используя полученные значения оценок параметров модели, вычисляются значения оценок эндогенной переменной для каждой точки контрольной выборки.

4) Формулируется статистическая гипотеза о равенстве реального и прогнозного значений эндогенной переменной в каждой точке контрольной выборки:

.

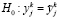5) Вычисляются значения статистик Стьюдента или границы доверительных интервалов для каждой контрольной точки, и проверяется условие принятия гипотезы об адекватности

После всех этих вычислений получается следующий результат:

Критерий Стьюдента: 2,018081679.

Статистическая гипотеза об адекватности модели принимается с вероятностью Рдов=0,95. Это подтверждают результаты тестирования, как с помощью статистики Стьюдента, так и с помощью доверительных интервалов.

Выводы

Также используя результаты регрессионного анализа ранжировать регионы по эффективности (по остаткам). Для этого необходимо выполнить сортировку по остаткам. В результате ранжировки получаем следующие данные (3 наиболее и наименее эффективных региона):

Итак, наиболее эффективным субъектом по заработной плате является Московская область, а наименее – Камчатский край.

На основании построенной модели регрессии ранжируем факторы по степени их влияния на зависимую переменную с помощью коэффициентов эластичности, β- и α-коэффициентов [3].

Данные коэффициенты высчитываются по следующим формулам:

; ;

.

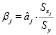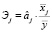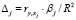Получаем следующие значения:

Коэффициент эластичности показывает: при увеличении среднего размера назначенной пенсии на 1%, средняя заработная плата увеличивается на 1,4%. При увеличении численности занятых в экономике, приходящихся на одного пенсионера на 1%, средняя заработная плата увеличится на 0,7%. При увеличении потребительских расходов в среднем на душу населения на 1%, средняя заработная плата увеличится на 0,27%.

Построение доверительного интервала и анализ наблюдений

«Бета-коэффициент показывает, на какую часть величины среднеквадратического отклонения Sy изменится зависимая переменная Y, если соответствующая независимая переменная Xj изменится на величину своего квадратичного отклонения при фиксированном значении остальных независимых переменных» [3].

Дельта оценивает долю влияния каждого фактора в суммарном влиянии всех факторов.

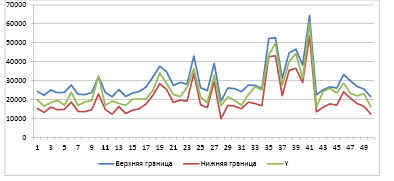
Заключительным пунктом моей работы является построение доверительного интервала и анализ наблюдений, которые выходят за верхние или нижние границы (рисунок).

Только в одном субъекте (Московская область) зарплата выше средней заработной платы по регионам.

Данный субъект Российской Федерации имеет большую среднюю заработную плату, так как он находится в непосредственной близости со столицей и, следовательно, уровень жизни выше, чем в других регионах.