Мультиколлинеарность – это явление, при котором существует линейная связь между всеми или несколькими объясняющими переменными, что приводит к уменьшению точности оценивания переменных или даже к невозможности оценивания. Основная причина в том, что при наличии мультиколлинеарности переменные становятся зависимыми, поэтому становится невозможным выделение воздействия каждой из объясняющих переменных на зависимую. Наличие мультиколлинеарности является одной из основных причин неустойчивости регрессионных моделей. Одним из способов устранения мультиколлинеарности и повышения устойчивости модели является отбор наиболее значимых признаков. Проблема мультиколлинеарности, возможные способы её обнаружения и устранения описаны в [1, 2, 3, 6]. Также мультиколлинеарность приводит к уменьшению устойчивости оценок вектора параметров. Оценка вектора параметров называется устойчивой, если малое изменении некоторой компоненты этого вектора приводит к малому изменению соответствующей компоненты оценки целевого вектора.
В своей работе мы взяли данные по российским банкам и решили сравнить модели, полученные в результате исследования отдельно банков Московской и Ленинградской областей (включая города Москва и Санкт-Петербург). Мы использовали несколько способов определения мультиколлинеарности и избавления от нее. В качестве зависимой переменной y были признаны активы банков, а 11 факторов, которые будут представлены ниже – в качестве объясняющих переменных.
Актуальность работы обусловлена тесной связью банковской сферы России с экономическими событиями, происходящими в нашей стране. Целью работы стали выявление и исследование факторов, оказывающих наибольшее влияние на активы банков в Московской и Ленинградской областях. Для достижения цели были поставлены следующие задачи:
1. Проверить данные на наличие мультиколлинеарности;
2. Построить многофакторные модели, максимально избавившись от мультиколлинеарности;
3. Провести сравнительный анализ полученных результатов.
Для того, чтобы показать как можно больше способов определения и избавления от мультиколлинеарности, при анализе Московской и Ленинградской области эти способы отличались.
Определение мультиколлинеарности
в массиве данных:
Построим матрицу парных коэффициентов корреляции (табл. 1, 2).
Таблица 1
А) Для Московской области
|
Активы |
Валюта баланса |
Прибыль до налогов |
Депозиты частных лиц |
Вложения в государственные ценные бумаги |
Вложения в негосударственные ценные бумаги |
Средства в банках (брутто) |
Кредиты небанковскому сектору |
Просроченные кредиты небанковскому сектору |
Кредиты физическим лицам |
Обязательства перед банками |
Иностранные обязательства |
|
|
Х1 |
Х2 |
Y |
Х3 |
Х4 |
Х5 |
Х6 |
Х7 |
Х8 |
Х9 |
Х10 |
Х11 |
|
|
Х1 |
1 |
|||||||||||
|
Х2 |
0,994 |
1 |
||||||||||
|
Y |
0,951 |
0,978 |
1 |
|||||||||
|
Х3 |
0,967 |
0,98 |
0,98 |
1 |
||||||||
|
Х4 |
0,96 |
0,98 |
0,99 |
0,98 |
1 |
|||||||
|
Х5 |
0,93 |
0,898 |
0,807 |
0,83 |
0,83 |
1 |
||||||
|
Х6 |
0,83 |
0,785 |
0,688 |
0,729 |
0,701 |
0,854 |
1 |
|||||
|
Х7 |
0,997 |
0,997 |
0,965 |
0,978 |
0,971 |
0,91 |
0,785 |
1 |
||||
|
Х8 |
0,83 |
0,797 |
0,698 |
0,769 |
0,734 |
0,86 |
0,816 |
0,81 |
1 |
|||
|
Х9 |
0,95 |
0,959 |
0,94 |
0,98 |
0,935 |
0,82 |
0,748 |
0,958 |
0,795 |
1 |
||
|
Х10 |
0,98 |
0,96 |
0,898 |
0,91 |
0,914 |
0,96 |
0,870 |
0,967 |
0,891 |
0,90 |
1 |
|
|
Х11 |
0,87 |
0,825 |
0,714 |
0,734 |
0,7396 |
0,907 |
0,7705 |
0,853 |
0,751 |
0,728 |
0,88 |
1 |
Таблица 2
Б) Для Ленинградской области
|
Активы |
Валюта баланса |
Прибыль до налогов |
Депозиты частных лиц |
Вложения в государственные ценные бумаги |
Вложения в негосударственные ценные бумаги |
Средства в банках (брутто) |
Кредиты небанковскому сектору |
Просроченные кредиты небанковскому сектору |
Кредиты физическим лицам |
Обязательства перед банками |
Иностранные обязательства |
|
|
Y |
Х1 |
X2 |
Х3 |
Х4 |
Х5 |
Х6 |
Х7 |
Х8 |
Х9 |
Х10 |
Х11 |
|
|
Y |
1 |
|||||||||||
|
Х1 |
0,98 |
1 |
||||||||||
|
X2 |
0,998 |
0,986 |
1 |
|||||||||
|
Х3 |
0,169 |
0,189 |
0,18 |
1 |
||||||||
|
Х4 |
0,162 |
0,316 |
0,21 |
0,26 |
1 |
|||||||
|
Х5 |
0,998 |
0,981 |
1 |
0,2 |
0,194 |
1 |
||||||
|
Х6 |
0,999 |
0,973 |
1 |
0,13 |
0,125 |
0,995 |
1 |
|||||
|
Х7 |
1 |
0,983 |
1 |
0,19 |
0,184 |
0,999 |
0,997 |
1 |
||||
|
Х8 |
0,998 |
0,969 |
0,99 |
0,15 |
0,104 |
0,994 |
0,999 |
0,996 |
1 |
|||
|
Х9 |
0,031 |
0,041 |
0,04 |
0,97 |
0,145 |
0,053 |
-0 |
0,049 |
0,02 |
1 |
||
|
Х10 |
0,998 |
0,97 |
0,99 |
0,14 |
0,109 |
0,995 |
1 |
0,996 |
1 |
0 |
1 |
|
|
Х11 |
0,997 |
0,968 |
0,99 |
0,11 |
0,099 |
0,992 |
0,999 |
0,994 |
1 |
-0,02 |
0,999 |
1 |
Мультиколлинеарность существует, когда коэффициент парной корреляции > 0,8. Можно заметить, что значений, превышающих необходимое требование много. Соответственно, в рассматриваемом примере существует мультиколлинеарность. Для определения наличия мультиколлинеарности используются различные методы.
Для определения мультиколлинеарности используем метод Белсли. Belsley, Kuh и Welsch предложили метод анализа мультиколлинеарности основанный на индексах обусловленности (the scaled condition indexes) и дисперсионных долях (the variance-decomposition proportions) [2].
При численном решении различных прикладных задач исследователи часто сталкиваются с таким понятием как число обусловленности. Это понятие описывается в учебниках по матричной алгебре [5]. Число обусловленности η является важнейшим «индикатором» для определения устойчивости решения той или иной задачи.
Обусловленность оценивает близость матрицы коэффициентов к вырожденной. Число обусловленности η является количественной оценкой обусловленности. Отметим, что всегда η > 1. Если η > 103, то говорят, что матрица плохо обусловлена. Если 1 < η < 100, то матрица считается хорошо обусловленной.
Оценки собственных значений получены в программе VSTAT. Вычислим 11 коэффициентов обусловленности по формуле ηj = μmax / μj. В нашем примере показатель обусловленности η равен 416,247. Следовательно, можно сделать вывод о наличии зависимости близкой к линейной между столбцами матрицы Х, т.е. о наличии мультиколлинеарности (табл. 3).
Таблица 3
Коэффициенты обусловленности
|
Фактор |
Собств. значение (l) λj = μj2 |
μ |
ή |
|
|
1 |
9,313549546 |
3,051811 |
1 |
|
|
2 |
1,08pic5728384 |
1,041983 |
2,92885 |
|
|
3 |
0,254369927 |
0,504351 |
6,05097 |
|
|
4 |
0,192395949 |
0,43863 |
6,9576 |
|
|
5 |
0,073098285 |
0,270367 |
11,2877 |
|
|
6 |
0,045620985 |
0,213591 |
14,2881 |
|
|
7 |
0,026pic565880 |
0,16299 |
18,7239 |
|
|
8 |
0,004414457 |
0,066441 |
45,9324 |
|
|
9 |
0,002707pic560 |
0,052034 |
58,6501 |
|
|
10 |
0,001495273 |
0,038669 |
78,9219 |
|
|
11 |
0,000053754 |
0,007332 |
416,247 |
Метод дополнительных регрессий (Тест VIF).
Для измерения эффекта мультиколлинеарности используется показатель VIF – «фактор инфляции вариации»:
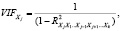
где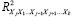 
– это значение коэффициента множественной корреляции, полученное для регрессора Xj как зависимой переменной и остальных переменных. При этом степень мультиколлинеарности, представляемая в регрессии переменной Xj, когда все переменные X включены в регрессию, есть функция множественной корреляции между Xj и другими переменными X (табл. 4, 5).
Таблица 4
А) Для Московской области
|
VIF |
1 |
2 |
3 |
4 |
5 |
|
Значение |
1432,32 |
211,37 |
387,71 |
153,47 |
26,1131 |
|
VIF |
6 |
7 |
8 |
9 |
10 |
11 |
|
Значение |
11,8380 |
806,792 |
13,9070 |
90,5577 |
102,679 |
34,8001 |
Такие большие значения свидетельствуют о наличии мультиколлинеарности.
Таблица 5
Б) Для Ленинградской области
|
VIFx1 |
VIFx2 |
VIFx3 |
VIFx4 |
VIFx5 |
VIFx6 |
|
117,437 |
1553,46 |
54,1101 |
65,2989 |
10774,4 |
10774,4 |
|
VIFx7 |
VIFx8 |
VIFx9 |
VIFx10 |
VIFx11 |
|
8617,59 |
8971,33 |
38,3602 |
95674,6 |
29214,6 |
На основании только данного способа построение уравнения регрессии представляется затруднительным в силу того, что все показатели вздутия регрессии по всем факторам принимают очень большие значения.
Используем пошаговый метод избавления от мультиколлинеарности (табл. 6, 7, 8).
Таблица 6
А) Для Московской области
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
Нижние 95,0% |
Верхние 95,0% |
|
|
Активы |
656377,9 |
320869,2 |
2,04562419 |
0,0413729 |
25793,484 |
1286962,2 |
25793,48472 |
1286962,24 |
|
Валюта баланса |
0,034053 |
0,004782 |
7,12161243 |
4,248E-12 |
0,024655 |
0,0434491 |
0,024655793 |
0,0434498 |
|
Прибыль до налогов |
-3,73084 |
0,342514 |
-10,892541 |
1,09E-24 |
-4,403964 |
-3,057722 |
-4,40396448 |
-3,0577229 |
|
Депозиты частных лиц |
-0,04382 |
0,017078 |
-2,pic5656506 |
0,0106203 |
-0,07737 |
-0,010253 |
-0,0773792 |
-0,0102539 |
|
Вложения в государственные ценные бумаги |
0,981389 |
0,107064 |
9,1663929 |
1,736E-18 |
0,770982 |
1,1917942 |
0,77098273 |
1,1917942 |
|
Вложения в негосударственные ценные бумаги |
0,669773 |
0,019868 |
33,7117500 |
2,58E-125 |
0,6307283 |
0,7088176 |
0,630728374 |
0,7088176 |
|
Средства в банках (брутто) |
0,912039 |
0,012199 |
74,764229 |
2,97E-256 |
0,8880657 |
0,9360130 |
0,88806pic5716 |
0,9360130 |
|
Кредиты небанковскому сектору |
1,111184 |
0,014478 |
76,748008 |
5,29E-261 |
1,0827307 |
1,1396375 |
1,082730792 |
1,13963757 |
|
Просроченные кредиты небанковскому сектору |
-0,45274 |
0,053391 |
-8,4796615 |
3,251E-16 |
-0,5pic571004 |
-0,340052 |
-0,55766004 |
-0,3478100 |
|
Кредиты физическим лицам |
0,023151 |
0,01pic561 |
1,483061419 |
0,1387pic56537 |
-0,007526862 |
0,053828576 |
-0,007526862 |
0,053828576 |
|
Обязательства перед банками |
0,151825 |
0,025522 |
5,94869445 |
5,427E-09 |
0,101667 |
0,2019825 |
0,101667371 |
0,2019825 |
|
Иностранные обязательства |
-0,05632 |
0,021472 |
-2,6227674 |
0,0090171 |
-0,098511 |
-0,014112 |
-0,09851192 |
-0,0141182 |
|
t значение |
1,965237 |
Таблица 7
Исключаем фактор «Кредиты физическим лицам», потому что tрасч<tтабл по модулю.
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
Нижние 95,0% |
Верхние 95,0% |
|
|
Активы |
676056,2 |
321019,9 |
2,10596362 |
0,0357583 |
45179,50 |
1306932,8 |
45179,503 |
1306932,82 |
|
Валюта баланса |
0,033152 |
0,004749 |
6,98054992 |
1,057E-11 |
0,023818 |
0,0424846 |
0,023818406 |
0,04248462 |
|
Прибыль до налогов |
-3,66193 |
0,339797 |
-10,776818 |
2,948E-24 |
-4,32970 |
-2,994142 |
-4,3297037 |
-2,9941492 |
|
Депозиты частных лиц |
-0,02504 |
0,011476 |
-2,1818304 |
0,0296364 |
-0,047592 |
-0,002485 |
-0,047592 |
-0,0024857 |
|
Вложения в государственные ценные бумаги |
0,89814 |
0,09129 |
9,8383641 |
7,969E-21 |
0,718735 |
1,0775441 |
0,718735036 |
1,0775441 |
|
Вложения в негосударственные ценные бумаги |
0,664487 |
0,019pic571 |
33,952281 |
1,92E-126 |
0,626024 |
0,702948 |
0,626024889 |
0,70294854 |
|
Средства в банках (брутто) |
0,915277 |
0,012018 |
76,159332 |
5,5E-260 |
0,891658 |
0,9388945 |
0,891658648 |
0,9388945 |
|
Кредиты небанковскому сектору |
1,113918 |
0,01438 |
77,465463 |
4,43E-263 |
1,08pic5659 |
1,1421772 |
1,08pic56591 |
1,1421772 |
|
Просроченные кредиты небанковскому сектору |
-0,43523 |
0,052139 |
-8,3475pic550 |
8,568E-16 |
-0,53769 |
-0,332765 |
-0,537693 |
-0,3327652 |
|
Обязательства перед банками |
0,150313 |
0,025536 |
5,8863376 |
7,703E-09 |
0,100128 |
0,2004962 |
0,100128846 |
0,2004962 |
|
Иностранные обязательства |
-0,05314 |
0,021393 |
-2,4839806 |
0,0133535 |
-0,095181 |
-0,011097 |
-0,0951815 |
-0,0110976 |
|
t значение |
1,965226 |
Теперь все факторы значимые: не проходят через 0, адекватные стандартные ошибки и сопоставимое значение t-статистики. Можем составлять модель: y = 676056,2 + 0,033152 × х1 – 3,66193 × х2 – 0,02504 × х3 + 0,89814 × х4 + 0,664487 × х5 + 0,915277 × х6 + 1,113918 × х7 – 0,43523 × х8 + 0,150313 × х10 – 0,05314 × х11.
Несмотря на то, что модель составлена, переменные поменяли знак при анализе, значит, эта модель не имеет смысла – пошаговый метод не справился с избавлением от мультиколлинеарности.
При пошаговом методе были исключены следующие факторы: депозиты частных лиц, вложения в государственные ценные бумаги, прибыль до налогов.
Таблица 8
А) Для Ленинградской области
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
Нижние 95,0% |
Верхние 95,0% |
|
|
Y-пересечение |
68pic551,1 |
203468,9 |
0,336912 |
0,738254 |
-344947 |
482050 |
-344947,4 |
482049,6 |
|
Валюта баланса |
0,005735 |
0,000947 |
6,054548 |
7,32E-07 |
0,00381 |
0,00766 |
0,00381 |
0,00766 |
|
Вложения в негосударственные ценные бумаги |
1,092755 |
0,084623 |
12,9132 |
1,15E-14 |
0,92078 |
1,26473 |
0,920779 |
1,264729 |
|
Средства в банках (брутто) |
1,0pic56923 |
0,066691 |
15,84797 |
2,87E-17 |
0,92139 |
1,19246 |
0,921389 |
1,192456 |
|
Кредиты небанковскому сектору |
0,917211 |
0,023789 |
38,pic5pic5651 |
1,2E-29 |
0,868867 |
0,96pic556 |
0,868866 |
0,965555 |
|
Просроченные кредиты небанковскому сектору |
4,979605 |
0,725254 |
6,866013 |
6,62E-08 |
3,50pic5711 |
6,4535 |
3,50pic5710 |
6,453498 |
|
Кредиты физическим лицам |
0,249733 |
0,066758 |
3,740865 |
0,000676 |
0,114064 |
0,3854 |
0,114064 |
0,385401 |
|
Обязательства перед банками |
-0,31542 |
0,096694 |
-3,26208 |
0,00252 |
-0,51193 |
-0,1182 |
-0,511928 |
-0,118917 |
|
Иностранные обязательства |
0,484714 |
0,164696 |
2,943094 |
0,005819 |
0,150013 |
0,81942 |
0,150012 |
0,819415 |
|
tтабл |
2,728394 |
|||||||
|
Табличное значение критерия стьюдента: tтабл = (a=0,01; df=n-k-1=43-8-1) = 34 |
||||||||
Таблица 9
|
Активы |
Валюта баланса |
Вложения в негосударственные ценные бумаги |
Средства в банках (брутто) |
Кредиты небанковскому сектору |
Просроченные кредиты небанковскому сектору |
Кредиты физическим лицам |
Обязательства перед банками |
Иностранные обязательства |
|
181834540 |
424106466 |
24063371 |
52667821 |
93100261 |
3700977 |
2198913 |
5,7E+07 |
22811820 |
|
314260202 |
733473633 |
42027740 |
92628367 |
1,61E+08 |
6523656 |
3256250 |
1E+08 |
41505209 |
Первая строка – среднее
Вторая строка – среднеквадратическое отклонение
Таблица 10
|
Активы |
Валюта баланса |
Вложения в негосударственные ценные бумаги |
Средства в банках (брутто) |
Кредиты небанковскому сектору |
Просроченные кредиты небанковскому сектору |
Кредиты физическим лицам |
Обязательства перед банками |
Иностранные обязательства |
|
|
Активы |
1 |
0,980 |
0,998 |
0,99885 |
0,99957 |
0,99821 |
0,03043 |
0,9982 |
0,99665 |
В этом случае нам удалось избавиться от мультиколлинеарности
Полученная модель
Y = 68551 + 0,0057X1 + 1,0928X2 + 1,0928X5 + 1,0569X6+ 0,9172X7 + 4,9796X8 + 0,2497X9 – 0,315X10 + 0,4847X11
Проверим качество полученной модели (табл. 9, 10).
Долю влияния фактора в суммарном влиянии всех факторов можно оценить по величине дельта – коэффициентов дельта j:
|
дельта1 |
дельта 5 |
дельта6 |
дельта7 |
|
0,013341 |
0,000124 |
2,39Е-0,7 |
2,39E-07 |
|
дельта 8 |
дельта9 |
дельта 10 |
дельта11 |
|
8,17E-05 |
2,43E-06 |
0,001285 |
0,00102 |
Наибольшее влияние на результирующий показатель оказывают просроченные кредиты небанковскому сектору, однако мы должны учесть высокую степень волатильности этого фактора, что было показано в предыдущем расчете
Наименьший результат и здесь снова принадлежит фактору вложений в негосударственные ценные бумаги.
Делая выводы о качестве данной модели необходимо заметить, что коэффициент детерминации принимает большое значение, что говорит нам о том, что в модель было включено подавляющее большинство факторов, оказывающих значительно влияние на итоговый показатель. Коэффициенты эластичности показывают, что именно такие факторы, как объем кредитов, выданных физическим лицам, объем кредитов небанковскому сектору, объем просроченных кредитов имеют наибольший эффект для накопления банков активов.
Тест Фаррара – Глоубера из 3х последовательных процедур:
В результате проведенных расчётов были получены следующие данные:
А) Для Московской области:
|
FG набл |
14501,10476 |
61,65623338 |
Fgтабл |
FGнабл > FGкрит, Hо отклоняеся, факторы признаются коллинеарными. В массиве есть коллинеарность.
|
F1 |
F2 |
F3 |
|
62098,78 |
9105,807513 |
7656,165574 |
|
F4 |
F5 |
F6 |
|
4863,41902 |
1070,423867 |
461,2419851 |
|
F7 |
F8 |
F10 |
F11 |
|
34958,60566 |
539,2204578 |
4476,832858 |
1475,324 |
Так как все F > Fтабл, то соответствующие переменные Х мультиколлинеарны друг с другом.
После исключения факторов имеем модель:
y = 268715 + 0,319194 × х3 + 0,800632 × х7 + 1,732275 × х10 + 0,656838 × х11,
в которой коэффициент эластичности равен 3,52%, а R^2 = 0,816, что свидетельствует о высокой точности и хорошем качестве полученной модели.
Интерпретируя модель, можно сказать, что основными факторами, которые влияют на активы банков в Москве и Московской области, являются депозиты частных лиц, кредиты небанковскому сектору, обязательства перед банками и иностранные обязательства. Достаточно странно, что фактор «кредиты физическим лицам» был исключен в ходе построения модели, но, тем не менее, это можно связать с тем, что столичные банки очень тесно связаны с корпоративными клиентами, фирмами и бизнесом. Крупные кредиты на развитие бизнеса выдаются именно в крупных банках, чаще всего государственных, которые сосредоточены как раз в Москве. Так же в столице развит рынок межбанковских кредитов, поэтому фактор «обязательства перед банками» оказывает сильное прямое воздействие на размер активов.
Б) Для Ленинградской области:
Проверив наличие мультиколлинеарности всего массива переменных, выяснили, что FGнабл > FGкрит, факторы признаются коллинеарными. Так же переменные оказались мультиколлинеарными друг с другом.
После исследования мультиколлинеарности и исключения факторов с целью избавления от нее, была получена следующая модель:
Y = -1986523,164 + 2,02X7 – 2,23X9
Отрицательный знак при Х9 и свободном члене является явным признаком признаком того, что результат, показываемый данной моделью, может быть искаженным, даже принимая во
|
дельта7 |
дельта 9 |
|
1,033510199 |
-0,0006605 |
Наибольшее влияние на Y оказывает также объем кредитов небанковскому сектору.
Наименьший результат и здесь снова принадлежит фактору вложений в негосударственные ценные бумаги.
Заключение
Целью нашей работы было исследование и сравнение факторов, влияющих на величину активов банков Московской и Ленинградской области.
На активы банков Московской области больше всего влияют такие факторы, как депозиты частных лиц, кредиты небанковскому сектору, обязательства перед банками и иностранные обязательства. Ф «кредиты физическим лицам» был исключен в ходе составления модели, однако это объясняется тем, что в Москве сосредоточены крупные государственные банки, которые дают много кредитов небанковскому сектору и в которые аккумулируют значительные сбережения населения.
На активы банков Ленинградской области больше всего влияют такие факторы, как депозиты частных лиц, кредиты небанковскому сектору, обязательства перед банками и иностранные обязательства.
Таким образом, несмотря на некоторые различия, наблюдаются значительные сходства. Во-первых, это объясняется тем, что в Московской и Ленинградской областях есть спрос на банковские услуги одного типа. Во-вторых, это ключевые области Российской Федерации, где сосредоточены все виды бизнеса, которые нуждаются в банковском кредитовании. В-третьих, именно в Москве и Санкт-Петербурге больше всего развиты международные обязательства, поэтому фактор «иностранные обязательства» играет важное и ключевое значение при выявлении влияния факторов на активы банков.