Согласно проведенным исследованиям в оценке эффективности результатов бизнеса большую помощь могут оказать математические модели, позволяющие осуществить следующие возможности [1]:
• исследование свойств системы (объекта);
• контроль динамики развития системы (объекта);
• создание интегрированных систем управления и контроля системы;
• оптимизация параметров функционирования системы;
• осуществление финансово-экономического анализа результатов деятельности организации;
• прогнозирование будущих состояний и перспектив развития системы (объекта управления).
Оценка параметров математических моделей является определяющим моментом, от которого в большой степени зависит качество построенной математической модели и, в конечном итоге, качество построенного по модели прогноза и эффективность управленческих решений с использованием результатов прогнозирования [2].
Одним из наиболее распространенных методов оценки параметров математических моделей является метод наименьших квадратов и его различные модификации. Этот метод довольно часто применяется при обработке экспериментальных данных, создании и оценке экономических и социальных моделей. Этот математический метод помогает решать задачу подбора параметров функции для приближённого описания зависимости величины результативного признака от величины факторных признаков, оказывающих влияние на результативный признак.
Первичные экономические данные, полученные экспериментальным путем или из материалов официальной статистической отчетности, могут касаться различных отраслей экономики и науки, и к тому же, могут содержать различного рода ошибки, связанные как со стохастической природой экономических данных, так и с неизбежными техническими погрешностями при измерении и обработке информации. В сфере экономики это могут быть исследования зависимости показателей безработицы и инфляции, зависимости роста безработицы, зависимости цены товара от спроса на этот товар, зависимости частного потребления от располагаемого дохода и т.д. Как видим, сферы использования математических методов достаточно широкие [3].
Общематематический прием, который используется с целью разрешения разнообразных заданий и базируется на минимизировании суммы квадратов отклонений математических значений от переменных, подлежащих установлению, называют методом наименьших квадратов (англ. Ordinary Least Squares, OLS). Метод наименьших квадратов применяется в том случае, когда число уравнений превосходит число неизвестных, в случае обычных (не переопределенных) нелинейных систем уравнений, для замены точечных функций определенным математическим значением и т.д.
Метод наименьших квадратов определяют как способ моделирования диагностируемых показателей, изучение их признаков в целях анализа незнакомых величин по результатам измерений, которые имеют случайные ошибки. Суть МНК состоит в нахождении коэффициентов линейной зависимости, при которой функция двух переменных a и b обретает наименьшее значение. Именно при данных a и b сумма квадратов отклонений пробных данных от установленной прямой будет наименьшей.
Одними из ученых, которые впервые использовали в изучении системы уравнений теорию вероятностей, стали Лежандр (1805-1906) и Гаусс (1794-1895). Примененный ими прием помогает определить вероятнейшие значения, но не определяет верных смыслов данных. Поэтому дальнейшие работы Лапласа, Энке, Бесселя, Ганзена и других авторов довели прием до совершенства. Прием был назван методом наименьших квадратов.
Использование метода наименьших квадратов отмечается также и в области налогооблажения. Здесь используется шкала регрессии ставок единого социального налога агентами, выплачивающими налоги в соответствии с Налоговым кодексом Российской Федерации. Можно наблюдать использование данного метода для приближенного представления заданной функции новыми простыми функциями, такое применение эффективно при обработке экспериментальных наблюдений, т.е. МНК широко используется в статистике. В интеллектуальном анализе данных (Data Mining), оценка параметров регрессии применяется для разрешения вопросов прогнозирования и численного предсказания показателей сложных экономических процессов [4].
Таким образом, благодаря своей сравнительной простоте и результативности метод наименьших квадратов является в наибольшей степени исследованным и популярным, находящим широкое применение для оценки параметров эконометрических моделей, характеризующих экономические процессы как на макроуровне, так и на уровне отдельных организаций (микроуровне) [5].
Рассмотрим пример использования метода наименьших квадратов для оценки параметров модели зависимости товарооборота фирмы от размера торговых площадей. Статистические данные по годовому товарообороту и торговым площадям компании «ССК-Смол», имеющей сеть, состоящую из 12 оптовых складов, представлена в таблице. При исследовании ставится задача выявить зависимость годового товарооборота от площади складских помещений. Для выполнения расчетов используем MS Excel [6].
Обозначим yt – годовой товарооборот t-го склада, млн. руб; x1t – площадь n-го склада, тыс. м².
Построим диаграмму рассеивания анализируемых показателей (рисунок) для определения формы функциональной зависимости между товарооборотом и площадью складских помещений.
Статистические данные товарооборота компании «ССК-Смол»
|
№ склада |
Товарооборот годовой, млн. руб |
Площадь склада, тыс. м² |
|
1 |
197,6 |
2,4 |
|
2 |
380,9 |
3,1 |
|
3 |
409,5 |
5,5 |
|
4 |
410,8 |
4,8 |
|
5 |
562,9 |
7,8 |
|
6 |
685,1 |
9,8 |
|
7 |
750,1 |
9,4 |
|
8 |
890,5 |
12,1 |
|
9 |
911,3 |
12,9 |
|
10 |
912,6 |
11,2 |
|
11 |
998,4 |
12,9 |
|
12 |
1085,5 |
14,9 |
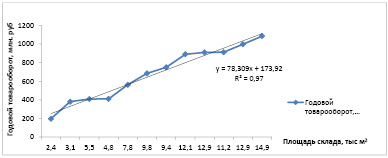
График зависимости товарооборота от площади склада
На основании построенной диаграммы можно сделать вывод о прямой положительной связи между yt и x1t , т.е. с ростом площади склада годовой товарооборот также растет. Между анализируемыми показателями установлена функциональная связь – линейная, о качестве которой свидетельствует высокое значение коэффициента детерминации, равного 0,97. Построение диаграммы рассеивания можно осуществить, как используя MS Excel, так и ряд специализированных программ статистического анализа и прогнозирования [7].
С помощью МНК (метода наименьших квадратов) оцененное уравнение линейной однофакторной эконометрической модели имеет вид:
Y(t)t =173,92+78,309·x(t)
Можно сделать вывод, что при увеличении площади склада на 1 тыс. м², при других неизменных условиях, среднегодовой товарооборот возрастет на 78,309 млн. руб. Таким образом, для увеличения товарооборота целесообразно и дальнейшее увеличение площади складских помещений.

