В работе проводится экономико-математический анализ показателей бухгалтерской финансовой отчетности Открытого акционерного общества «Газпром» за период с 1998г. по 2013г. Целью работы является построение адекватной эконометрической модели для выражения связи между величиной прибыли компании и отдельными статьями ее баланса. Актуальность данной работы заключается в возможности применения полученных результатов для принятия управленческих решений для стратегического планирования финансовой деятельности компании.
В качестве исходных данных используется бухгалтерская финансовая отчетность ОАО «Газпром» за 15-летний период, опубликованная на сайте компании [4]. Отчетность за указанные периоды была экспортирована в Excel для дальнейшего проведения эконометрического анализа.
Согласно цели исследования, работа посвящена выявлению степени влияния отдельных статей бухгалтерского баланса на финансовый результат компании, т.е. величину чистой прибыли компании. Таким образом, в качестве эндогенной (результирующей) переменной был выбран показатель «чистая прибыль». В качестве экзогенных переменных были выбраны показатели: «долгосрочные обязательства», «краткосрочные обязательства», «оборотные активы», «внеоборотные активы», «капитал и резервы» (табл. 1).
Для начала построим диаграммы для того, чтобы наглядно проследить за взаимосвязью между переменными. Из них следует, что с ростом показателей отдельных статей баланса в среднем чистая прибыль компании «Гарзпром» растет.
Для определения взаимосвязи между экзогенными переменными построим матрицу парных коэффициентов корреляции. Получим таблицу 2.
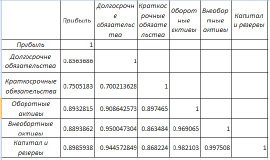
Все факторы имеют тесную взаимосвязь с результирующим признаком. Таким образом, из исходных данных можно установить явление мультиколлинеарности, так как коэффициенты парной корреляции между переменными за исключением «краткосрочных обязательств» больше 0,8.
Чтобы избавиться от мультиколлинеарности, в модель включают лишь один из функционально связанных между собой факторов, причем тот, который в большей степени связан с зависимой переменной.
Используем регрессионный анализ для определения наиболее значимого фактора в модели. В первую модель включаем все выбранные факторы, кроме «краткосрочных обязательств», так как у данного фактора наименьший коэффициент парной корреляции, и используем инструмент анализа данных «регрессия». После первой итерации из модели выводим фактор «внеоборотные активы», т.к. коэффициент при данном факторе имеет минимальное значение (-0,24). На втором шаге исключается фактор «капитал и резервы», коэффициент при котором равен 0,04. Мы получаем 2-факторную модель, но фактор «долгосрочные обязательства» несущественен, так как верхние и нижние границы интервала проходят через 0. В итоге, получаем модель с одним значимым фактором «оборотные активы» (рисунок).
Таблица 1
Исходные данные
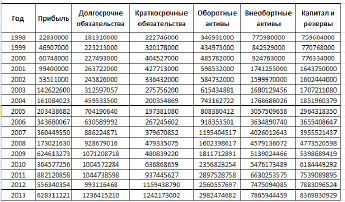
Таблица 2
Матрица парных коэффициентов корреляции
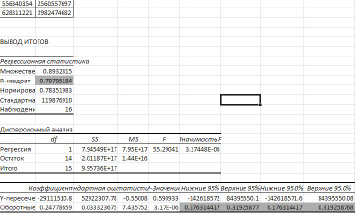
Модель с одним значимым фактором «оборотные активы»
В результате было получено следующее уравнение регрессии:
Y=-29111510.78+0.247787*X,
где X – оборотные средства;
Дадим экономическую интерпретацию полученным коэффициентам:
• С увеличением оборотных средств на 1 млн. руб. чистая прибыль компании вырастет на 247 787 руб.
Из регрессионного анализа следует, что коэффициент детерминации (R^2) равен 0,8 .Это означает, что прибыль компании «Газпром» на 80% зависит от количества оборотных активов и на 20% – от прочих факторов.
Сравним расчетное значение критерия Фишера с табличным: для этого используем формулу СТЬЮРАСПОБР (0,01;14). Получим F расчетное равное 55,29, а табличное 2,98. Fрасч. > Fтабл. Следовательно, уравнение статистически значимо.
Оценим уровень точности модели по стандартной ошибке модели
.
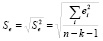Для этого необходимо сравнить её со среднеквадратическим отклонением результативного признака Y
.
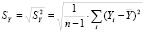Из протокола регрессии, Se=119876910,25. Среднеквадратическое отклонение Y равно 257647824. Sy>Se, т.е. можем утверждать, что полученная модель статистически точна.
Далее оценим степень влияния экзогенной переменной на результирующую переменную «Чистая прибыль» с помощью коэффициента эластичности, и бета-коэффициента.
Коэффициент эластичности показывает, на сколько процентов изменяется зависимая переменная при изменении фактора на один процент и находится по формуле:
,
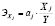где aj – коэффициент регрессии, перед фактором Xj в уравнении регрессии.
Бета-коэффициент показывает, на какую часть величины среднеквадратического отклонения меняется среднее значение зависимой переменной с изменением независимой переменной на одно СКО при фиксированном на постоянном уровне значении остальных независимых переменных и находятся по формуле
,
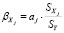где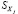
, 
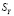– среднеквадратические отклонения выбранных переменных.
Рассчитаем данные коэффициенты для нашей модели:
|
Коэффициенты |
Обор. активы |
|
эластичность |
1.098606719 |
|
Бета (β) |
0.8932815 |
Значения коэффициентов определяют, что:
• Показатель «чистая прибыль» эластичен по фактору «оборотные активы» (1,1).
• При изменении фактора на одно среднеквадратическое отклонение, чистая прибыль изменяется на 0,89 всего среднеквадратического отклонения соответственно.
Из анализа коэффициентов эластичности и β-коэффициента, можно сделать вывод о сильном влиянии на результирующую переменную фактора «оборотные активы». Иными словами, ОАО «Газпром» более рационально использовать механизм увеличения оборотных активов для привлечения прибыли.
В работе был произведен эконометрический анализ показателей финансовой бухгалтерской отчетности ОАО «Газпром» за 15 летний период. Была выявлена взаимосвязь между показателями статей баланса компании. Таким образом, был определен источник для лучшего финансирования деятельности компании, максимизации ее финансового результата. Модель статистически значима и точна, следовательно, выводы, полученные в результате проведенного анализа, рекомендованы для применения на практике.