Econometrics is a field of economics that concerns itself with the application of mathematical statistics and is a tool of statistical inference to empirical measurement of relations postulated by economic theory. Thus, it helps analyzing various economic phenomena, forecast their development and predict future fluctuations. The purpose of this work is to analyze the Klein’s Investment function. And can it be used to analyze the investments in Switzerland. And understand how if there is any influence on investment from GDP and Interest rate. The initial equation of the Klein’s Investment function looks like this:
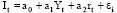
In this research work I have constructed econometric models of this function for the analysis of the Gross capital formation formerly gross domestic investments and the influence of GDP and Interest rate on its value.
The Initial form of our model that we estimate in this work is:
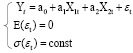
Where,
Y – is the Gross Capital Formation or just Gross domestic investment. That can de defined as outlays on additions to the fixed assets of the economy plus the net changes in the level of the inventories.
X1 – is Gross Domestic Product that is defined by OECD as an aggregate measure of production equal to the sum of the gross values added of all resident institutional units engaged in production (plus any taxes, and minus any subsidies, on products not included in the value of their outputs).
X2 – is interest rate is the rate at which interest is paid by a borrower (debtor) for the use of money that they borrow from a lender (creditor). Specifically, the interest rate (I/m) is a percentage of principal (P) paid a certain number of times (m) per period (usually quoted per year). For example, a small company borrows capital from a bank to buy new assets for its business, and in return the lender receives interest at a predetermined interest rate for deferring the use of funds and instead lending it to the borrower. Interest rates are normally expressed as a percentage of the principal for a period of one year.
With the halp of Correlation matrix observes the relations between all the variables. The strongest relation is between Investment and GDP, we can easily determine it because their correlation is close to 1. In economic sense it means that when the GDP is growing the all welfare of the country increases and provide more preferable conditions for investment that why it also increase, or vice versa when we increase the investment in country it can have a positive influence on GDP. The relation between Investment and Interest rate is not so strong, as we can see in the matrix their correlation is close to 0,5, and have the negative influence because of the mines before the numbers. This negative relation in explained that when the interest rate is increases less people want to make investments, that why it fall. Correlation matrix is a very useful tool, because not only can it tell the relationship between exogenous and endogenous variable, but it shows the dependence between each variable in response to all others presented in the matrix.
Further we can analyze our problem by regression analysis. Regression explores the linear relationship between the dependent variables (Ii) and independent variables (Yt;rt). Using these results we check our model.
The first test is R-test. R2 in the linear regression shows what extend of the variations of the dependent variable are explained by the model. The result shows that R2 is equal to:
Switzerland: R2= 0,991
R^2 regression is more than 0,9, which means that more than 99% of all variations of the dependent variables are explained by the independent variables included in the model and only near 1% are the results of the other sources such as random error or variables not included in the model.
Next test is F-Test. In F-test, F critical was calculated by estimating the degree of freedom(regression df and residual df) and observation parameters. F critical should be compared to F calculated in a model by Excel. If the result of this comparison is F calculated>F critical, then determination coefficient R² is not random and thus, the model has a good quality of specification.
Switzerland: F=976,061>6,11
As the F-stat is higher that F-crit we can conclude that R-square is not random and the quality of specification of our econometric models is high.
Another test is T-test which helps us to determine if estimated coefficients are significant or not. First of all we need to calculate T-crit and compare with T-stat.
Switzarland:
StatY=4,089> t-crit coefficient is significant
StatX1=38,355> t-crit coefficient is significant
StatX2=4,00555> t-crit coefficient is significant
Now we can make the conclusion that only in Switzerland all variables are significant.
In order to check that standard deviation of the disturbance term is constant, Which means that residuals are homoscedastic and there is no overestimation of the model results, we need to pass GQ test. For implementing the GQ-test, all data must be sorted in ascending order of addition absolute values of Xs. Then the sorted data is divided into distinct data sets and they are analyzed respectively. Regression models are built for separate data sets, in a similar way as for the initial model. It is clear, that F critical is calculated again for new data sets and this value is compared to GQ and 1/GQ values. It is important to understand, that GQ=ESS1(ESS of a model for new data set 1)/ESS2(ESS of a model for new data set 2).
To check this conditions we should calculate F-crit of GQ and compare with ESS1/ESS2 and RSS2/RSS1.
Switzerland
|
ESS1/ESS2 |
0,965 |
|
ESS2/ESS1 |
1,035 |
|
Fcrit |
2,784 |
After the analysis of the result we can see that GQ test is passed (Fcrit>GQ;Fcrit>1/GQ) and it means that residuals are homoscedastic and we can use OLS technique in order to estimate parameters of the model. Gauss-Markov condition is confirmed – standard deviation of disturbance term is constant.
In order to check the autocorrelation in the residuals we need to pass Durbin-Watson test. Here we need to use the DW table of statistics to determine dl and du and the interval scopes of critical values to construct the intervals from 0 to 4. If the value of DW lays between du and 4-du we can claim that there is no auto-correlation in the residuals. The intervals between dl –du and 4-dl – 4-du is the intervals of uncertainty where we cant be sure we there is autocorrelation of the residuals or not. And intervals between 0-dl and 4-dl-0 is the intervals where we have autocorrelation in our model.
The table of Durbin-Watson critical values for 2 independent variables and 20 observations shows that dl=0,872 du=1,27
Switzerland DW=1,345
0 dl(0,872) du(1,27) 2 4-du(2,73) 4-dl(3,128) 4
Looking on the results of DW stat for all countries we see that Switzerland have negative autocorrelation in the residuals as the value of DW lays in the interval between du – 4-du, so we can use linear model for estimation of coefficients.
Now we need to check the adequacy of the model for every country we need to make forecasts of Investments for 2012, which will be based on our model and compare with the real figures. We need to calculate Y theoretical and lower and upper boundaries and check if the Yth lays between them. IN order to calculate Yth for all countries we need substitute actual values of X1 and X2 into linear equation with estimated coefficients. After that, a confidence interval should be introduced in order to evaluate, whether real value of endogenous variable for the last years observed fits into that interval, built on the created model.
Confidence interval consists of higher and lower theoretical values of Y, each defined by this formulas:
Lower boundary is calculated as Yth-tcrit*st.error
Upper boundary is calculated as Tth+tcrit*st.error
Switzerland:
|
Yth= |
84719,22 |
|
y-= |
82513,79 |
|
y+= |
86924,66 |
|
Yreal= |
83842,00 |
This model is adequate and can be used for predictions.
Now we can calculate the error of our predictions Using the Y real and Y th we calculate it by using this formula Error=(Yth-Yreal)/Yth
Switzerland: 0,0103
Analyzing the result we see error is small, it means that our model make pretty good predictions of future values.
Now after all tests and calculation are made, we can write down estimated forms of the model
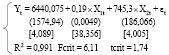
Conclusion
Test results shows that Switzerland passes all the test it don’t have insignificant coefficients, their residuals are homoscedastic and have positive autocorrelation that means that all Gauss-Markov conditions are confirmed and also its model is adequate and can make proper prediction with small error. It means that Kleins Investment model can be used for predictions of investment in Switzerland. This explains that Investment can be determent by two variables GDP and Interest rate also we see that when GDP is growing investment rise as well but relation between Investment and Interest rate is negative. After the calculation if Theoretical value of Investment for year 2012 we estimate it as 84719,22 bll $ that is very close to real value. And we see the trend of growth in investment in Switzerland it is probably because it is highly developed country with stable economy. And it have stable Inflow of investment that is continue to grow because of perspective conditions for profit and good investment environment.

