Металлические силосы применяются в качестве универсального хранилища в сельском хозяйстве, строительной, химической и пищевой промышленности в различных производствах для приема, хранения и передачи сыпучих веществ, например, песка, цемента, гипса, извести, зерна, муки и другого мелкодисперсного гранулированного материала. Они могут устанавливаться как отдельно стоящими, так и представлять единый комплекс силосных корпусов. Силосная емкость устанавливается на металлическую опорную раму, высота которой зависит от конструкции силоса и целей его использования. На него монтируется различное технологическое оборудование (датчики уровней, вибраторы, рукавные фильтры и аэрационные устройства, предназначенные для равномерного распределения продукта внутри емкости и обеспечения текучести продукта во время его отпуска, моечные головки, краны отбора проб, смотровые стекла, воздуховоды и т.д.).
Несущие конструкции в большинстве случаев представляют собой элементы двутаврового или коробчатого сечения (в зависимости от объема силоса и насыпной плотности материала), подверженные внецентренному сжатию или сжатию с изгибом.
Мы попытались проанализировать напряженно-деформированное состояние (НДС) элементов коробчатого сечения по аналогии с [1-4]. Модуль деформаций назначаем следующим образом: при упругой работе принимаем его равным модулю упругости стали (Е = 2⋅105 МПа); при упруго-пластической – вводим условный модуль Ех
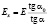 ,
,
где tgα – тангенс фактического угла наклона линии деформации к горизонту и tgα0 – тангенс аналогичного угла, который мог иметь место, если бы деформации были упругими и вычислялись по закону Гука. Условный модуль Ex меняется по длине зоны пластического деформирования. После определения модуля Ех, прогиб в рассматриваемой точке вычисляется с помощью интеграла Мора
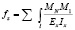 .
.
Из условия равновесия внешних и внутренних сил и моментов в каждом сечении элемента определяются напряжения и деформации. При этом рассматривается диаграмма работы стали с эллиптическим участком между пределом пропорциональность и пределом текучести и принимается гипотеза плоских сечений. Анализируя общий случай расчетной эпюры напряжений вместо краевых деформаций оказалось более удобным определять пропорциональные им условные напряжения:
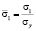 ,
, 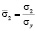 ,
, 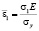 ,
, 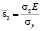
На кромках сечения напряжения полагаем равными условным – в случае упругой работы материала и равными пределу текучести – в случае пластической работы. Упругопластический участок сечения разбивался на 10 частей, в пределах которых результирующие усилия и координаты их приложения определялись численным методом.
При односторонней текучести (рисунок)
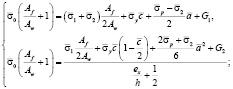
где
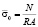 ,
, 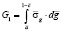 ,
, 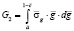 ,
, 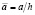 ,
, 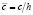 ,
, 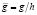 и g –
и g –
координаты волокон с деформациями превышающими εp, но не достигающими εy.
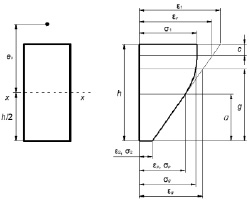
Эпюры деформаций и напряжений опоры силоса
Для вычисления прогибов элементов использовался метод последовательных приближений. Алгоритм расчета был следующим:
Коробчатый несущий элемент разбивается на 100 отрезков равной длины.
В первом приближении вычисляются упругие балочные прогибы (с учетом опорных точек).
Определяются моменты внешних сил и краевые деформации в тех же точках при полученных прогибах.
Для каждого из отрезков уточняются модули Ех.
С помощью интеграла Мора вычисляются прогибы в середине каждого отрезка с найденными моментами и уточненными модулям Ех.
Программа возвращается к пункту 3 алгоритма с полученными прогибами до достижения заданной точности расчета.
Результаты анализа НДС выводятся на экран монитора и печать.
В заключение следует отметить, что использование данной методики для моделирования напряженно-деформированного состояния, позволяет оценивать резервы несущей способности и рассчитывать опорные элементы силосов.

